
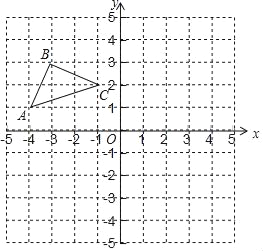
【题目】如图,△ABC三个顶点的坐标分别为A(1,1)、B(4,2)、C(3,4).
(1)请画出△ABC向左平移5个单位长度后得到的△A1B1C1;
(2)请画出△ABC关于x轴对称的△A2B2C2三个顶点A2、B2、C2的坐标;
(3)在x轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出P的坐标.

 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源: 题型:
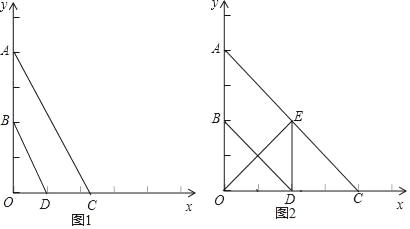
【题目】已知:如图,平面直角坐标系中,A(0,4),B(0,2),点C是x轴上一点,点D为OC的中点.
(1)求证:BD∥AC;
(2)若点C在x轴正半轴上,且BD与AC的距离等于1,求点C的坐标;
(3)如果OE⊥AC于点E,当四边形ABDE为平行四边形时,求直线AC的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某品牌A,B两种型号冰箱的销售情况,王明对某专卖店一到七月份的销售情况进行了统计,并将得到的数据制成如下统计表:
月份 | 一月 | 二月 | 三月 | 四月 | 五月 | 六月 | 七月 |
A型销 售量(台) | 10 | 14 | 17 | 16 | 13 | 14 | 14 |
B型销 售量(台) | 6 | 10 | 14 | 15 | 16 | 17 | 20 |
完成下表:
平均数(台) | 中位数(台) | 方差 | |
A型销售量 | 14 | ||
B型销售量 | 14 | 18.6 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景:
小红同学在学习过程中遇到这样一道计算题“计算4×3.142﹣4×3.14×3.28+3.282”,他觉得太麻烦,估计应该有可以简化计算的方法,就去请教崔老师.崔老师说:你完成下面的问题后就可能知道该如何简化计算啦!
获取新知:
请你和小红一起完成崔老师提供的问题:
(1)填写下表:
x=﹣1,y=1 | x=1,y=0 | x=3,y=2 | x=1,y=1 | x=5,y=3 | |
A=2x﹣y | ﹣3 | 2 | 4 | 1 | 7 |
B=4x2﹣4xy+y2 | 9 | 4 |
|
|
|
(2)观察表格,你发现A与B有什么关系?
解决问题:
(3)请结合上述的有关信息,计算4×3.142﹣4×3.14×3.28+3.282.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一个底面为菱形的直棱柱,高为10cm,体积为150cm3 , 则这个棱柱的下底面积为cm2;若该棱柱侧面展开图的面积为200cm2 , 记底面菱形的顶点依次为A,B,C,D,AE是BC边上的高,则CE的长为cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是市民广场到解百地下通道的手扶电梯示意图.其中AB、CD分别表示地下通道、市民广场电梯口处地面的水平线,∠ABC=135°,BC的长约是 ![]() m,则乘电梯从点B到点C上升的高度h是 m.
m,则乘电梯从点B到点C上升的高度h是 m.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点O为坐标原点,已知△ABC三个定点坐标分别为A(﹣4,1),B(﹣3,3),C(﹣1,2).
(1)画出△ABC关于x轴对称的△A1B1C1,点A,B,C的对称点分别是点A1、B1、C1,直接写出点A1,B1,C1的坐标;
(2)画出点C关于y轴的对称点C2,连接C1C2,CC2,C1C,求△CC1C2的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高学生书写汉字的能力,增强保护汉子的意识,某校举办了首届“汉字听写大赛”,学生经选拔后进入决赛,测试同时听写100个汉字,每正确听写出一个汉字得1分,本次决赛,学生成绩为![]() (分),且
(分),且![]() ,将其按分数段分为五组,绘制出以下不完整表格:
,将其按分数段分为五组,绘制出以下不完整表格:
组别 | 成绩 | 频数(人数) | 频率 |
一 |
| 2 | 0.04 |
二 |
| 10 | 0.2 |
三 |
| 14 | b |
四 |
| a | 0.32 |
五 |
| 8 | 0.16 |
(1)本次决赛共有 名学生参加;
(2)直接写出表中a= ,b= ;
(3)请补全下面相应的频数分布直方图;

(4)若决赛成绩不低于80分为优秀,则本次大赛的优秀率为 。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com