【题目】已知一个底面为菱形的直棱柱，高为10cm，体积为150cm3 ， 则这个棱柱的下底面积为cm2；若该棱柱侧面展开图的面积为200cm2 ， 记底面菱形的顶点依次为A，B，C，D，AE是BC边上的高，则CE的长为cm．

参考答案：

【答案】15；1或9
【解析】解：∵底面为菱形的直棱柱，高为10cm，体积为150cm3 ， ∴这个棱柱的下底面积为：150÷10=15（cm2）；
∵该棱柱侧面展开图的面积为200cm2 ， 高为10cm，
∴底面菱形的周长为：200÷10=20（cm），
∴AB=BC=CD=AD=20÷4=5（cm），
∴AE=S菱形ABCD÷BC=15÷5=3（cm），
∴BE= =4（cm），
∴如图1：EC=BC﹣BE=5﹣4=1（cm），
如图2：EC=BC+BE=5+4=9（cm），
所以答案是：15；1或9．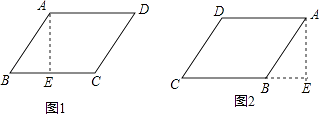

【考点精析】解答此题的关键在于理解认识立体图形的相关知识，掌握有些几何图形的各个部分不都在同一平面内，它们是立体图形，以及对几何体的展开图的理解，了解沿多面体的棱将多面体剪开成平面图形，若干个平面图形也可以围成一个多面体；同一个多面体沿不同的棱剪开，得到的平面展开图是不一样的，就是说：同一个立体图形可以有多种不同的展开图．

关闭