
【题目】用同样大小的围棋子按如图所示的方式摆图案,按照这样的规律摆下去,第12个图案的围棋子个数是( )

A. 16 B. 28 C. 29 D. 38
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,点A、D、C、F在同一条直线上,AD=CF,AB=DE,BC=EF.
(1)求证:ΔABC≌△DEF;
(2)若∠A=55°,∠B=88°,求∠F的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=90°,∠A=30°.

(1)用尺规作图作AB边上的中垂线DE,交AC于点D,交AB于点E.(保留作图痕迹,不要求写作法和证明);
(2)连接BD,求证:BD平分∠CBA.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】邻边不相等的平行四边形纸片,剪去一个菱形,余下一个四边形,称为第一次操作;在余下的四边形纸片中再剪去一个菱形,又剩下一个四边形,称为第二次操作;…依此类推,若第n次操作余下的四边形是菱形,则称原平行四边形为n阶准菱形.如图1,ABCD中,若AB=1,BC=2,则ABCD为1阶准菱形.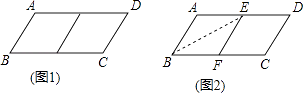
(1)判断与推理:
①邻边长分别为2和3的平行四边形是阶准菱形;
(2)小明为了剪去一个菱形,进行了如下操作:如图2,把ABCD沿BE折叠(点E在AD上),使点A落在BC边上的点F,得到四边形ABFE.请证明四边形ABFE是菱形.
(3)操作、探究与计算:
①已知ABCD的邻边长分别为1,a(a>1),且是3阶准菱形,请画出ABCD及裁剪线的示意图,并在图形下方写出a的值;
②已知ABCD的邻边长分别为a,b(a>b),满足a=6b+r,b=5r,请写出ABCD是几阶准菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店甲、乙两种商品三天销售情况的账目记录如下表:
日期 | 卖出甲商品的数量(个) | 卖出乙商品的数量(个) | 收入(元) |
第一天 | 39 | 21 | 321 |
第二天 | 26 | 14 | 204 |
第三天 | 39 | 25 | 345 |
(1)财务主管在核查时发现:第一天的账目正确,但其他两天的账目有一天有误,请你判断第几天的账目有误,并说明理由;
(2)求甲、乙两种商品的单价.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,平面直角坐标系中,A(0,4),B(0,2),点C是x轴上一点,点D为OC的中点.
(1)求证:BD∥AC;
(2)若点C在x轴正半轴上,且BD与AC的距离等于1,求点C的坐标;
(3)如果OE⊥AC于点E,当四边形ABDE为平行四边形时,求直线AC的解析式.
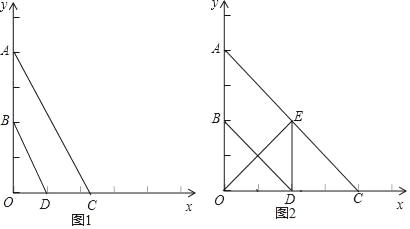
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)①观察一列数1,2,3,4,5,…,发现从第二项开始,每一项与前一项之差是一个常数,这个常数是 ;根据此规律,如果![]() (
(![]() 为正整数)表示这个数列的第
为正整数)表示这个数列的第![]() 项,那么
项,那么![]() ,
,![]() ;
;
②如果欲求![]() 的值,可令
的值,可令
![]() ……………①
……………①
将①式右边顺序倒置,得![]() ……………②
……………②
由②加上①式,得2![]() ;
;
∴ S=_________________;
由结论求![]() ;
;
(2)①观察一列数2,4,8,16,32,…,发现从第二项开始,每一项与前一项之比是一个常数,这个常数是 ;根据此规律,如果![]() (
(![]() 为正整数)表示这个数列的第
为正整数)表示这个数列的第![]() 项,那么
项,那么![]() ,
,![]() ;
;
②为了求![]() 的值,可令
的值,可令![]() ,则
,则![]() ,因此
,因此![]() ,所以
,所以![]() ,
,
即![]() .
.
仿照以上推理,计算![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A(4,0),O为坐标原点,P是线段OA上任意一点(不含端点O,A),过P、O两点的二次函数y1和过P、A两点的二次函数y2的图象开口均向下,它们的顶点分别为B、C,射线OB与AC相交于点D.当OD=AD=3时,这两个二次函数的最大值之和等于( )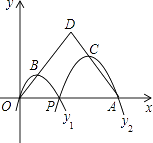
A.![]()
B.![]()
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一个底面为菱形的直棱柱,高为10cm,体积为150cm3 , 则这个棱柱的下底面积为cm2;若该棱柱侧面展开图的面积为200cm2 , 记底面菱形的顶点依次为A,B,C,D,AE是BC边上的高,则CE的长为cm.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com