练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】计算：

    （1）（﹣20）+（+3）﹣（﹣5）

    （2）（﹣5）×6×÷（﹣2）

    （3）﹣÷﹣×（﹣9）

    （4）（﹣1）4+5÷（﹣）×（﹣6）

    （5）（+﹣）×36

    （6）﹣1﹣[1+（﹣12）÷6]×（﹣）

    【答案】（1）﹣12；（2）9；（3）4；（4）181；（5）26；（6）．

    【解析】

    （1）根据有理数的加减法法则进行计算即可；

    （2）根据有理数的乘除法法则进行计算即可；

    （3）根据有理数的乘除法和减法法则按运算顺序进行计算即可；

    （4）根据有理数的乘方、有理数的乘除法和加法法则进行计算即可；

    （5）根据乘法分配律进行计算即可；

    （6）根据有理数的乘除法和加减法法则进行计算即可.

    （1）（﹣20）+（+3）﹣（﹣5）

    ＝（﹣20）+3+5

    ＝﹣12；

    （2）（﹣5）×6×÷（﹣2）

    ＝5×6×

    ＝9；

    （3）﹣÷﹣×（﹣9）

    ＝

    ＝﹣2+6

    ＝4；

    （4）（﹣1）4+5÷（﹣）×（﹣6）

    ＝1+5×6×6

    ＝1+180

    ＝181；

    （5）（+﹣）×36

    ＝

    ＝27+20﹣21

    ＝26；

    （6）﹣1﹣[1+（﹣12）÷6]×（﹣）

    ＝﹣1﹣[1+（﹣2）]×（﹣）

    ＝﹣1﹣（）×（﹣）

    ＝﹣1﹣

    ＝．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，已知点A（4，0），O为坐标原点，P是线段OA上任意一点（不含端点O，A），过P、O两点的二次函数y1和过P、A两点的二次函数y2的图象开口均向下，它们的顶点分别为B、C，射线OB与AC相交于点D．当OD=AD=3时，这两个二次函数的最大值之和等于（ ）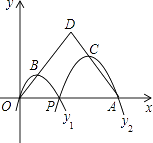

    A.
    B.
    C.3
    D.4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知一个底面为菱形的直棱柱，高为10cm，体积为150cm3 ， 则这个棱柱的下底面积为cm2；若该棱柱侧面展开图的面积为200cm2 ， 记底面菱形的顶点依次为A，B，C，D，AE是BC边上的高，则CE的长为cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图是市民广场到解百地下通道的手扶电梯示意图．其中AB、CD分别表示地下通道、市民广场电梯口处地面的水平线，∠ABC=135°，BC的长约是 m，则乘电梯从点B到点C上升的高度h是 m．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】探究：如图①，在Rt△ABC中，∠ACB=90°，AC=BC，直线l经过点C，且点A、B在直线l的同侧，过点A、B分别作直线l的垂线，垂足分别为点D、E．求证：DE=AD+BE．

    应用：如图②，在Rt△ABC中，∠ACB=90°，AC=BC，直线l经过点C，且点A、B在直线l的异侧，过点A、B分别作直线l的垂线，垂足分别为点D、E．直接写出线段AD、BE、DE之间的相等关系．

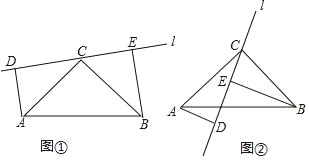
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，点O为坐标原点，已知△ABC三个定点坐标分别为A（﹣4，1），B（﹣3，3），C（﹣1，2）．

    （1）画出△ABC关于x轴对称的△A1B1C1，点A，B，C的对称点分别是点A1、B1、C1，直接写出点A1，B1，C1的坐标；

    （2）画出点C关于y轴的对称点C2，连接C1C2，CC2，C1C，求△CC1C2的面积．

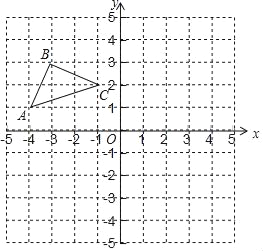
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知，在下列各图中，点 O 为直线 AB 上一点，∠AOC＝60°，直角三角板的直角顶点放在点处．

    （1）如图 1，三角板一边 OM在射线 OB 上，另一边 ON在直线 AB的下方，求∠BOC的度数，∠CON 的度数；

    （2）如图 2，三角板一边OM恰好在∠BOC的角平分线OE上，另一边ON在直线 AB的下方，求此时∠BON 的度数；

    （3）请从下列（A），（B）两题中任选一题作答． 我选择哪一题．

    （A）在图 2 中，延长线段 NO 得到射线 OD，如图 3，求∠AOD 的度数；写出∠DOC 与∠BON 的数量关系；

    （B）如图 4，MN⊥AB，ON 在∠AOC 的内部，若另一边 OM 在直线 AB 的下方， 求∠COM+∠AON 的度数；∠AOM﹣∠CON 的度数.

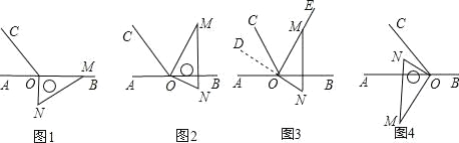
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，两个等腰直角△ABC和△CDE中，∠ACB=∠DCE=90°．

    （1）观察猜想如图1，点E在BC上，线段AE与BD的数量关系，位置关系．

    （2）探究证明把△CDE绕直角顶点C旋转到图2的位置，（1）中的结论还成立吗？说明理由；

    （3）拓展延伸：把△CDE绕点C在平面内自由旋转，若AC=BC=13，DE=10，当A、E、D三点在直线上时，请直接写出AD的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】中国古代数学家们对于勾股定理的发现和证明，在世界数学史上具有独特的贡献和地位，体现了数学研究中的继承和发展.现用4个全等的直角三角形拼成如图所示“弦图”.Rt△ABC中，∠ACB=90°，若，请你利用这个图形解决下列问题：

    （1）试说明；

    （2）如果大正方形的面积是10，小正方形的面积是2，求的值．

    查看答案和解析>>

    同步练习册答案