
����Ŀ����ƽ��ֱ������ϵ�ڣ������������Ͷ��κ���y=k��x2+x��1����ͼ���ڵ�A��1��k���͵�B����1����k����
��1����k=��2ʱ�����������Ľ���ʽ��
��2��Ҫʹ�����������Ͷ��κ�������y����x�������������kӦ����������Լ�x��ȡֵ��Χ��
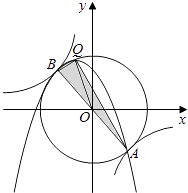
��3������κ�����ͼ��Ķ���ΪQ������ABQ����ABΪб�ߵ�ֱ��������ʱ����k��ֵ��
��4����CΪx����һ���㣬��C������Ϊ��2k��0��������ABC����ABΪб�ߵ�ֱ��������ʱ����K��ֵ��
���𰸡�
��1��
�⣺��k=��2ʱ��A��1����2����
��A�ڷ���������ͼ���ϣ�
���跴���������Ľ���ʽΪ��y= ![]() ��
��
����A��1����2�����2= ![]() ��
��
��ã�m=��2��
�෴���������Ľ���ʽΪ��y=�� ![]()
��2��
�⣺��Ҫʹ�����������Ͷ��κ�������y����x�����������
��k��0��
�߶��κ���y=k��x2+x��1��=k��x+ ![]() ��2��
��2�� ![]() k���Գ���Ϊ��ֱ��x=��
k���Գ���Ϊ��ֱ��x=�� ![]() ��
��
Ҫʹ���κ���y=k��x2+x��1������������������k��0������£�x�����ڶԳ������ߣ�
��x���� ![]() ʱ������ʹ��y����x�����������
ʱ������ʹ��y����x�����������
������������k��0��x���� ![]()
��3��
�⣺����һ��
�ɣ�2���ɵã�Q���� ![]() ����
���� ![]() k����
k����
�ߡ�ABQ����ABΪб�ߵ�ֱ�������Σ�A����B�����ԭ��Գƣ�
��ԭ��Oƽ��AB��
��OQ=OA=OB��
��BD��OC��QC��OC��

��OQ= ![]() =
= ![]() ��
��
��OB= ![]() =
= ![]() ��
��
�� ![]() =
= ![]() ��
��
��ã�k=�� ![]()
![]() ��
��
��������
�����ߵĶ���Q���� ![]() ����
���� ![]() k����A��1��k����B����1����k����
k����A��1��k����B����1����k����
�ߡ�ABQ����ABΪб�ߵ�ֱ�������Σ�
��AQ��BQ��
��KAQ��KBQ=��1��
�� 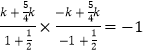 ��
��
�� ![]() ��
��
k1= ![]() ��k2=��
��k2=�� ![]() ��
��
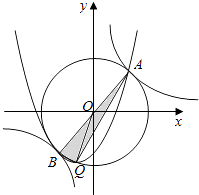
��4��
��ABC����ABΪб�ߵ�ֱ�������Σ�
��AC��BC��
��KAC��KBC=��1��
��A��1��k����B����1����k����C��2k��0����
�� ![]() ��
��
��3k2=1��
��k1= ![]() ��k2=��
��k2=�� ![]() ��
��
������������һ����1����k=��2ʱ��������õ�A�����꣬Ȼ���跴���������Ľ���ʽΪ��y= ![]() �����ô���ϵ����������ô𰸣���2���ɷ����������Ͷ��κ�������y����x����������ɵ�k��0�����ɶ��κ���y=k��x2+x��1���ĶԳ���Ϊx=��
�����ô���ϵ����������ô𰸣���2���ɷ����������Ͷ��κ�������y����x����������ɵ�k��0�����ɶ��κ���y=k��x2+x��1���ĶԳ���Ϊx=�� ![]() ���ɵ�x����
���ɵ�x���� ![]() ʱ������ʹ��y����x�����������3���ɡ�ABQ����ABΪб�ߵ�ֱ�������Σ�A����B�����ԭ��Գƣ�����ֱ��������б���ϵ����ߵ���б�ߵ�һ�룬���ɵ�OQ=OA=OB������Q����
ʱ������ʹ��y����x�����������3���ɡ�ABQ����ABΪб�ߵ�ֱ�������Σ�A����B�����ԭ��Գƣ�����ֱ��������б���ϵ����ߵ���б�ߵ�һ�룬���ɵ�OQ=OA=OB������Q���� ![]() ����
���� ![]() k����A��1��k�������ɵ�
k����A��1��k�������ɵ� ![]() =
= ![]() ���̶���ô𰸣�����������1���ԣ���2�����ݷ��������������κ����������Եó�k��x��ȡֵ��Χ����3�������Q�����꣬����ABΪб�ߣ��ó�AQ��ֱBQ�����ûƽ������ʽ�����⣮��4���г�A��B��C����������꣬���ûƽ������ʽ�����⣮
���̶���ô𰸣�����������1���ԣ���2�����ݷ��������������κ����������Եó�k��x��ȡֵ��Χ����3�������Q�����꣬����ABΪб�ߣ��ó�AQ��ֱBQ�����ûƽ������ʽ�����⣮��4���г�A��B��C����������꣬���ûƽ������ʽ�����⣮
�����㾫����������Ҫ�����˷��������������ʺͶ��κ��������ʵ����֪ʶ�㣬��Ҫ��������:��k��0ʱ˫���ߵ���֧�ֱ�λ�ڵ�һ���������ޣ���ÿ��������yֵ��xֵ���������С�� ��k��0ʱ˫���ߵ���֧�ֱ�λ�ڵڶ����������ޣ���ÿ��������yֵ��xֵ����������������ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С������ȷ�����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1�����۲�һ����1��2��3��4��5���������ִӵڶ��ʼ��ÿһ����ǰһ��֮����һ����������������� �����ݴ˹��ɣ����![]() ��
��![]() Ϊ����������ʾ������еĵ�
Ϊ����������ʾ������еĵ�![]() ���ô
���ô![]() ��
��![]() ��
��
���������![]() ��ֵ������
��ֵ������
![]() ������������
������������
����ʽ�ұ�˳���ã���![]() ������������
������������
����������ʽ����2![]() ��
��
�� S=_________________��
�ɽ�����![]() ��
��
��2�����۲�һ����2��4��8��16��32���������ִӵڶ��ʼ��ÿһ����ǰһ��֮����һ����������������� �����ݴ˹��ɣ����![]() ��
��![]() Ϊ����������ʾ������еĵ�
Ϊ����������ʾ������еĵ�![]() ���ô
���ô![]() ��
��![]() ��
��
��Ϊ����![]() ��ֵ������
��ֵ������![]() ����
����![]() �����
�����![]() ������
������![]() ��
��
��![]() .
.
������������������![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С������ڼ�μ����ʵ�������ij�����г���������ÿ��![]() Ԫ�ļ۸�
Ԫ�ļ۸�![]() ���ֻ���籦��Ȼ��ÿ���Ӽ�
���ֻ���籦��Ȼ��ÿ���Ӽ�![]() Ԫ���г����ۣ�
Ԫ���г����ۣ�
![]() ���۳�
���۳�![]() ���ֻ���籦�����ۼ�Ϊ����Ԫ������ú�
���ֻ���籦�����ۼ�Ϊ����Ԫ������ú�![]() ��
��![]() ��ʽ�ӱ�ʾ����
��ʽ�ӱ�ʾ����
![]() ���ڿ�ѧ�ٽ���С���ڳɹ��۳�
���ڿ�ѧ�ٽ���С���ڳɹ��۳�![]() ����籦������ʣ���籦���ۼ�
����籦������ʣ���籦���ۼ�![]() �۳��ۣ����ܿ�ȫ�����꣮
�۳��ۣ����ܿ�ȫ�����꣮
����Ȳ���ȡ�������ۣ�������ʵ�����۶�ӯ������Ԫ������ú�![]() ��
��![]() ��ʽ�ӱ�ʾ����
��ʽ�ӱ�ʾ����
����![]() ��С��ʵ��������������籦��������Ϊ________��������
��С��ʵ��������������籦��������Ϊ________��������![]() ����
����![]() ����
����![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ������Ϊ���ε�ֱ��������Ϊ10cm�����Ϊ150cm3 �� ������������µ����Ϊcm2��������������չ��ͼ�����Ϊ200cm2 �� �ǵ������εĶ�������ΪA��B��C��D��AE��BC���ϵĸߣ���CE�ij�Ϊcm��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
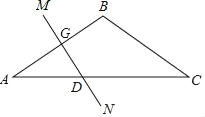
����Ŀ����ͼ���ڡ�ABC�У�BA=BC����B=120�����߶�AB�Ĵ�ֱƽ����MN��AC�ڵ�D����AD=8cm����
(1)��ADG�Ķ�����
(2)�߶�DC�ij��ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������㳡����ٵ���ͨ�����ַ�����ʾ��ͼ������AB��CD�ֱ��ʾ����ͨ��������㳡���ݿڴ������ˮƽ�ߣ���ABC=135�㣬BC�ij�Լ�� ![]() m����˵��ݴӵ�B����C�����ĸ߶�h�� m��
m����˵��ݴӵ�B����C�����ĸ߶�h�� m��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��̽������ͼ�٣���Rt��ABC�У���ACB=90�㣬AC=BC��ֱ��l������C���ҵ�A��B��ֱ��l��ͬ�࣬����A��B�ֱ���ֱ��l�Ĵ��ߣ�����ֱ�Ϊ��D��E����֤��DE=AD+BE��
Ӧ�ã���ͼ�ڣ���Rt��ABC�У���ACB=90�㣬AC=BC��ֱ��l������C���ҵ�A��B��ֱ��l����࣬����A��B�ֱ���ֱ��l�Ĵ��ߣ�����ֱ�Ϊ��D��E��ֱ��д���߶�AD��BE��DE֮�����ȹ�ϵ��
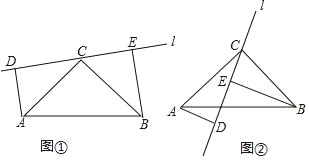
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�������и�ͼ�У��� O Ϊֱ�� AB ��һ�㣬��AOC��60�㣬ֱ�����ǰ��ֱ�Ƕ�����ڵ㴦��
��1����ͼ 1�����ǰ�һ�� OM������ OB �ϣ���һ�� ON��ֱ�� AB���·������BOC�Ķ�������CON �Ķ�����
��2����ͼ 2�����ǰ�һ��OMǡ���ڡ�BOC�Ľ�ƽ����OE�ϣ���һ��ON��ֱ�� AB���·������ʱ��BON �Ķ�����
��3��������У�A������B����������ѡһ������ ��ѡ����һ�⣮
��A����ͼ 2 �У��ӳ��߶� NO �õ����� OD����ͼ 3�����AOD �Ķ�����д����DOC ���BON ��������ϵ��
��B����ͼ 4��MN��AB��ON �ڡ�AOC ���ڲ�������һ�� OM ��ֱ�� AB ���·��� ���COM+��AON �Ķ�������AOM����CON �Ķ���.
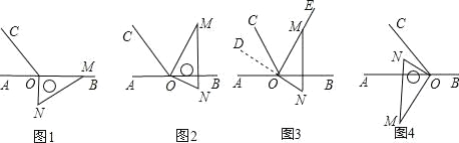
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�O������ԭ�㣬��A�������ǣ���2��4��������A��AB��y�ᣬ����ΪB������OA��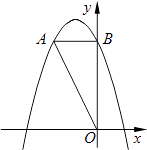
��1�����OAB�������
��2����������y=��x2��2x+c������A��
����c��ֵ��
�ڽ�����������ƽ��m����λ��ʹƽ�ƺ�õ��������߶������ڡ�OAB���ڲ�����������OAB�ı߽磩����m��ȡֵ��Χ��ֱ��д���𰸼��ɣ���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com