Question

【题目】如图，在△ABC中，BA=BC，∠B=120°，线段AB的垂直平分线MN交AC于点D，且AD=8cm．求：

(1)∠ADG的度数；

(2)线段DC的长度．

Answer 1

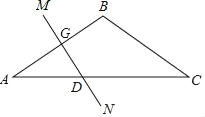
【答案】(1)∠ADG=60°；(2)DC=16cm．

【解析】

（1）根据等腰三角形的两个底角相等、三角形内角和定理来求∠A的度数；

（2）连接BD．根据线段垂直平分线的性质知△ABD是等腰三角形；然后利用（1）中的∠A=∠C=30°和已知条件∠B=120°可以推知△CDB是直角三角形，利用30度角所对的直角边是斜边的一半即可求得BD与CD间的数量关系；最后利用等腰三角形ABD的两腰相等（AD=BD）通过等量代换即可求得CD=2AD，从而求得线段DC的长度．

(1)在△ABC中，∵BA=BC，∴∠A=∠C（等边对等角）．

又∵∠B=120°，∴∠A=（180°﹣120°）=30°（三角形内角和定理），∴∠ADG=90°﹣30°=60°．

(2)连接BD．

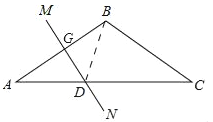
∵AB的垂直平分线DG交AC于点D，∴AD=BD，∠A=∠ABD=30°，∴∠CBD=90°．

由(1)知∠A=∠C=30°，∴BD=CD（30°所对的直角边是斜边的一半），∴CD=2AD=2BD．

又∵AD=8cm，∴DC=16cm．