
在△ABC与△A′B′C′中,已知AB<A′B′,BC<B′C′,CA<C′A′.下列结论:
(1)△ABC的边AB上的高小于△A′B′C′的边A′B′上的高;
(2)△ABC的面积小于△A′B′C′的面积;
(3)△ABC的外接圆半径小于△A′B′C′的外接圆半径;
(4)△ABC的内切圆半径小于△A′B′C′的内切圆半径.
其中,正确结论的个数为
 的等边三角形ABC和边长是6、8、10的直角三角形,求出其内切圆的半径都是5,即可判断(4)正确与否.
的等边三角形ABC和边长是6、8、10的直角三角形,求出其内切圆的半径都是5,即可判断(4)正确与否.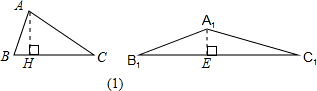
 解:(1)如图所示在△ABC与△A′B′C′中,已知AB<A′B′,BC<B′C′,CA<C′A′,但高AH>A1E,∴(1)错误;
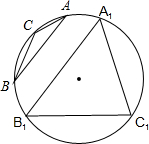
解:(1)如图所示在△ABC与△A′B′C′中,已知AB<A′B′,BC<B′C′,CA<C′A′,但高AH>A1E,∴(1)错误; 的等边三角形ABC,可根据勾股定理求出其内切圆的半径是5,同样作此圆的外切直角三角形A1B1C1,使三边长是6、8、10,符合已知条件,当两内切圆的半径相等,
的等边三角形ABC,可根据勾股定理求出其内切圆的半径是5,同样作此圆的外切直角三角形A1B1C1,使三边长是6、8、10,符合已知条件,当两内切圆的半径相等,

 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
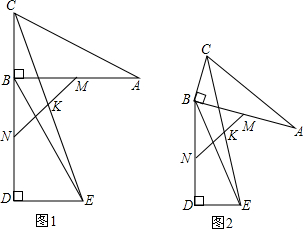
 如图,在△ABC与△AEF中,AB=AE,BC=EF,∠B=∠E,AB交EF于D.给出下列结论:
如图,在△ABC与△AEF中,AB=AE,BC=EF,∠B=∠E,AB交EF于D.给出下列结论:查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在△ABC与△DEF中,给出下列条件①
如图,在△ABC与△DEF中,给出下列条件①| AC |
| DF |
| BC |
| EF |
| AC |
| AB |
| DF |
| DE |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com