
【题目】如图,已知经过原点的抛物线y﹣ax2+bx+c(a≠0)的对称轴是直线x=﹣1,下列结论中:①ab>0,②a+b+c>0,③当﹣2<x<0时,y<0,正确的结论是 . 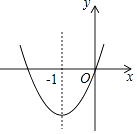
【答案】①②③
【解析】解:∵抛物线的开口向上, ∴a>0,
又∵对称轴在y轴的左侧,
∴b和a同号,即b>0,则ab>0,故①正确;
当x>0时,函数值大于0,则当x=1时,函数值是a+b+c>0,故②正确;
函数与x轴的一个交点是原点,对称轴是x=﹣1,则函数与x轴的另一交点是(﹣2,0).
则当﹣2<x<0时,y<0成立,故③正确.
故答案是:①②③.
【考点精析】利用二次函数图象以及系数a、b、c的关系和抛物线与坐标轴的交点对题目进行判断即可得到答案,需要熟知二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c);一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:初中数学 来源: 题型:
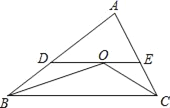
【题目】如图,△ABC中,点O是∠BCA与∠ABC的平分线的交点,过O作与BC平行的直线分别交AB、AC于D、E.已知△ABC的周长为15,BC的长为6,求△ADE的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B、E分别在直线AC和DF上,若∠AGB=∠EHF,∠C=∠D,可以证明∠A=∠F.请完成下面证明过程中的各项“填空”.

证明:∵∠AGB=∠EHF(理由: )
∠AGB= (对顶角相等)
∴∠EHF=∠DGF,∴DB∥EC(理由: )
∴ =∠DBA(两直线平行,同位角相等)
又∵∠C=∠D,∴∠DBA=∠D,
∴DF∥ (内错角相等,两直线平行)
∴∠A=∠F(理由: ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,DE∥AB.请根据已知条件进行推理,分别得出结论,并在括号内注明理由.

(1)∵DE∥AB,( 已知 )
∴∠2= . ( , )
(2)∵DE∥AB,(已知 )
∴∠3= .( , )
(3)∵DE∥AB(已知 ),
∴∠1+ =180°.( , )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,∠ABC=∠ADC,BF、DE分别平分∠ABC与∠ADC.∠1=∠3,求证:AB∥DC.
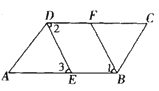
证明:∵∠ABC=∠ADC ( )
∴![]() ( )
( )
∵BF、DE分别平分∠ABC与∠ADC ( )
∴![]() ( )
( )
∴∠______=∠______ ( )
∵∠1=∠3( )
∴∠2=∠______ (等量代换)
∴____∥____ ( )
查看答案和解析>>
科目:初中数学 来源: 题型:
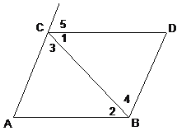
【题目】如图,完成下列推理过程,已知AB∥CD,AC∥BD,
(1)∵AB∥CD(已知) ∴∠A=∠5(两直线平行,_______________);
(2)∵AC∥BD(已知) ∴∠3=∠4(两直线平行,_______________);
(3)∵AB∥CD(已知) ∴∠__=∠___(两直线平行,內錯角相等);
(4)∵AB∥CD(已知) ∴∠D +∠______ =180°(两直线平行,____)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店用1000元购进一批套尺,很快销售一空;商店又用1500元购进第二批同款套尺,购进单价比第一批贵25%,所购数量比第一批多100套.
(1)求第一批套尺购进的单价;
(2)若商店以每套4元的价格将这两批套尺全部售出,可以盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学广场上有旗杆,在学习解直角三角形以后,数学兴趣小组测量了旗杆的高度.如图2,某一时刻,旗杆AB的影子一部分落在平台上,另一部分落在斜坡上,测得落在平台上的影长BC为4米,落在斜坡上的影长CD为3米,AB⊥BC,同一时刻,光线与水平面的夹角为72°,1米的竖立标杆PQ在斜坡上的影长QR为2米,求旗杆的高度(结果精确到0.1米).(参考数据:sin72°≈0.95,cos72°≈0.31,tan72°≈3.08) 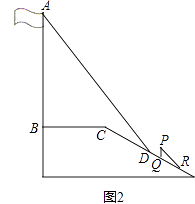
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com