

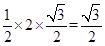 ;
;

 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源:不详 题型:解答题
 为对称轴作△ABC的轴对称图形△
为对称轴作△ABC的轴对称图形△ ;
; 可以看作是由△A1B1C1先向左平移4个单位,再以直线
可以看作是由△A1B1C1先向左平移4个单位,再以直线 为对称轴作轴对
为对称轴作轴对 还可以看作是由△A1B1C1经怎样变换得到的?请选择一种方法,写出图形变换的步骤。
还可以看作是由△A1B1C1经怎样变换得到的?请选择一种方法,写出图形变换的步骤。

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.(7,6) | B.(-2,0) | C.(4, 2) | D.(-10,0) |

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 的坐标分别为
的坐标分别为 ,将
,将 绕点
绕点 按逆时针方向旋转
按逆时针方向旋转 得到
得到 .
. ,并写出点
,并写出点 的坐标;
的坐标; 所经过的路径
所经过的路径 的长度.(结果保留
的长度.(结果保留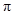 )
)
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 时,求CH的长。
时,求CH的长。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com