
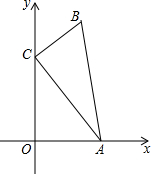
 如图,在△ABC中,∠ACB=90°,AC=8,BC=3,点A、C分别在x轴、y轴上,当点A在x轴上运动时,点C随之在y轴上运动,在运动过程中,点B到原点O的最大距离为
如图,在△ABC中,∠ACB=90°,AC=8,BC=3,点A、C分别在x轴、y轴上,当点A在x轴上运动时,点C随之在y轴上运动,在运动过程中,点B到原点O的最大距离为 解:作AC的中点D,连接OD、BD.
解:作AC的中点D,连接OD、BD.| BC2+CD2 |
| 32+42 |
| 1 |
| 2 |


科目:初中数学 来源: 题型:
| 模拟中招体育成绩(分数段)统计表 |  | ||
| 分数段 | 人数(人) | 频率 | |
| A | 60 | 0.2 | |
| B | a | 0.25 | |
| c | 90 | 0.30 | |
| D | 48 | b | |
| E | 27 | 0.09 | |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
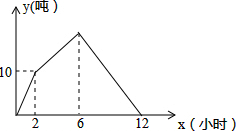 一个生产、装箱流水线,生产前没有积压产品,开始的2小时只生产,2小时后安排装箱(生产没有停止),6小时后生产停止只安排装箱,第12小时时生产流水线上刚好又没有积压产品,已知流水线的生产、装箱的速度保持不变,流水线上积压产品(没有装箱产品)y吨与流水线工作时间x(小时)之间的函数关系如图所示,则流水线上产品装箱的速度为
一个生产、装箱流水线,生产前没有积压产品,开始的2小时只生产,2小时后安排装箱(生产没有停止),6小时后生产停止只安排装箱,第12小时时生产流水线上刚好又没有积压产品,已知流水线的生产、装箱的速度保持不变,流水线上积压产品(没有装箱产品)y吨与流水线工作时间x(小时)之间的函数关系如图所示,则流水线上产品装箱的速度为查看答案和解析>>
科目:初中数学 来源: 题型:
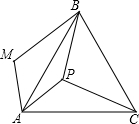 如图,P是正三角形ABC内的一点,且PA=6,PB=8,PC=10.若将△PAC绕点A逆时针旋转后,得到△MAB,则点P与点M之间的距离为
如图,P是正三角形ABC内的一点,且PA=6,PB=8,PC=10.若将△PAC绕点A逆时针旋转后,得到△MAB,则点P与点M之间的距离为查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com