
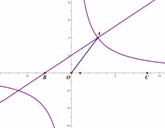
如图,在平面直角坐标系中,一次函数y=nx+2 (n≠0)的图像与反比例函数y= 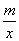 (m≠0)在第一象限内的图象交于点A,与x轴交于点B,线段OA=5,C为x轴
(m≠0)在第一象限内的图象交于点A,与x轴交于点B,线段OA=5,C为x轴 正半轴上一点,且Sin∠AOC=
正半轴上一点,且Sin∠AOC= 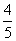
(1)  求一次函数和反比例函数的解析式
求一次函数和反比例函数的解析式
(2) 求△AOB的面积
(3)  直接写出不等式nx+2>
直接写出不等式nx+2>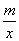 的解
的解
解:(1)过A点作AD⊥X轴于点D
∵sin∠AOC=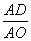 =
=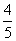 ,OA=5
,OA=5
∴AD=4
由勾股定理得OD=3
∴A坐标为(3,4)
将A点代入一次函数y=nx+2
与反比例函数y=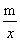 中得:
中得:
n= ,m=12
,m=12
∴一次函数为y= x+2
x+2
反比例函数为y= 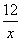 -----------------------------2分
-----------------------------2分
(2)在y= x+2中,令y=o即
x+2中,令y=o即 x+2=0
x+2=0
得x=-3
∴点B坐标为(-3,0)
∴OB=3 ∵AD=4
∴S△AOB=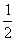 ·BO·AD
·BO·AD
=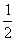 ·3·4
·3·4
=6
∴△AOB的面积为6 -----------------------------------------------------5分
(3)X>3或-6<X<0 -------------------------------------------------------7分


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
在四边形ABCD中,①AB∥CD,②AD∥BC,③AB=CD,④AD=BC,在这四个条件中任选两个作为已知条件,能判定四边形ABCD是平行四边形的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
函数 y=x2+bx+c与y=x的图像如图所示,有以下结论:
①b2-4c>0 ②b+c+1=0 ③3b+c+6=0
④当1<x<3时,x2+(b-1)x+c<0
其中正确的个数是( )
A、1 B、2 C、3 D、4
查看答案和解析>>
科目:初中数学 来源: 题型:
在平面直角坐标系中,∠AOB=30°,点A的坐标为(2,0),过点A作AA1⊥OB,垂足为点A1;过点A1作A1A2⊥X轴,垂足为点A2;过点A2⊥作A2A3⊥OB,垂足为点A3;过点A3做A3A4⊥X轴,垂足为点A4……,这样一直做下去,则A2013的纵坐标为
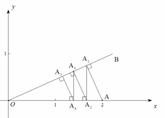
查看答案和解析>>
科目:初中数学 来源: 题型:
轴对称与轴对称图形
| 轴对称 | 轴对称图形 | |
| 定义 | 把一个图形沿某一条直线折叠,如果能够与另一个图形⑥ ,那么就说这两个图形成轴对称,这条直线就是⑦ ,两个图形的对应点叫做对称点. | 如果一个图形沿某条直线对折,对折的两部分能够完全⑧ ,那么就称这样的图形为轴对称图形,这条直线叫做这个图形的⑨ . |
| 区别 | 轴对称是指两个全等图形之间的相互位置关系. | 轴对称图形是指具有特殊形状的一个图形. |
| 轴对称的性质 | 1.对称点的连线被对称轴⑩ ; 2.对应线段⑪ ; 3.对应线段或延长线段的交点在⑫ 上; 4.成轴对称的两个图形⑬ . |
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,矩形ABCD中,AB=5,AD=12,将矩形ABCD按如图所示的方式在直线l上进行两次旋转,则点B在两次旋转过程中经过的路径的长是( )
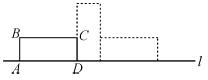
A.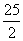 π B.13π C.25π D.25
π B.13π C.25π D.25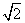
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com