
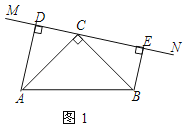
����Ŀ���ڡ�ABC�У���ACB=90�㣬AC=BC��ֱ��MN������C����AD��MN��D��BE��MN��E��
��1����ֱ��MN�Ƶ�C��ת��ͼ1��λ��ʱ
����˵����ADC�ա�CEB�����ɣ�
����˵��DE=AD+BE�����ɣ�
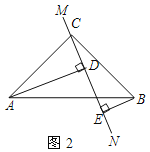
��2����ֱ��MN�Ƶ�C��ת��ͼ2��λ��ʱ��DE��AD��BE���������ĵ�����ϵ����ֱ���ں�����д�����������ϵ��__________��
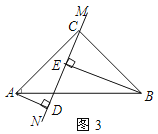
��3����ֱ��MN�Ƶ�C��ת��ͼ3��λ��ʱ��DE��AD��BE���������ĵ�����ϵ����ֱ���ں�����д�����������ϵ��__________��
���𰸡���1����֤������⣻��֤������⣻��2��DE=AD��BE����3��DE=BE��AD.
��������
��1���������������ACD+��BCE=90�㣬��DAC+��ACD=90�㣬����DAC=��BCE���ٸ���AAS���ɵ�֤��
�������õ�AD=CE��CD=BE�����ɵ�֤��
��2�����ƣ�1����֤�á�ACD=��EBC���Ƴ���ADC�ա�CEB����AD=CE��CD=BE��������֪���ɵô�𰸣�
��3��֤������ͬ��2��.
��1����֤������ͼ1�У�
��AD��DE��BE��DE��
���ADC=��BEC=90�㣬
�ߡ�ACB=90�㣬
���ACD+��BCE=90�㣬��DAC+��ACD=90�㣬
���DAC=��BCE��
����ADC����CEB��
 ��
��
���ADC�ա�CEB��AAS����
��֤��������֪��ADC�ա�CEB��
��AD=CE��CD=BE��
��DC+CE=DE��
��AD+BE=DE��
��2�����ۣ�DE=AD��BE��
����������
��ͼ2�У���BE��EC��AD��CE��
���ADC=��BEC=90�㣬
���EBC+��ECB=90�㣬
�ߡ�ACB=90�㣬
���ECB+��ACE=90�㣬
���ACD=��EBC��
�ڡ�ADC���CEB�У�
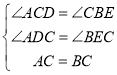 ��
��
���ADC�ա�CEB��AAS����
��AD=CE��CD=BE��
��DE=EC��CD=AD��BE��
��3�����ۣ�DE=BE��AD��
�������£���ͼ3�У��ߡ�ACB=90�㣬
���ACD+��BCE=90�㣬
�֡�AD��MN��BE��MN��
���ADC=��CED=90�㣬
���ACD+��DAC=90�㣬
���DAC=��ECB��
�ڡ�ACD���CBE�У�
 ��
��
���ACD�ա�CBE��AAS����
��AD=CE��CD=BE��
��DE=CD��CE=BE��AD.


 ȫ�ų��100��ϵ�д�
ȫ�ų��100��ϵ�д� Ӣ�ŵ��ϵ�д�
Ӣ�ŵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����̾�����ѧ����Ʒ������ÿ��280Ԫ�ļ۸�ij���ͺŵ�ѧϰ������ÿ��360Ԫ���ۼ�����ʱ��ÿ�¿��۳�60����Ϊ���������ۣ��þ����̲�ȡ���۵ķ�ʽ�������������з��֣����ÿ��ѧϰ������1Ԫ����ôÿ�¾Ϳ��Զ��۳�5����
![]() ����ǰ��������ѧϰ��ÿ�µ������Ƕ���Ԫ��
����ǰ��������ѧϰ��ÿ�µ������Ƕ���Ԫ��
![]() ��������������ѧϰ��ÿ�µ�����Ҫ�ﵽ7200Ԫ���Ҿ����������ڹ˿ͣ���ÿ��ѧϰ��Ӧ���۶���Ԫ��
��������������ѧϰ��ÿ�µ�����Ҫ�ﵽ7200Ԫ���Ҿ����������ڹ˿ͣ���ÿ��ѧϰ��Ӧ���۶���Ԫ��
![]() ��
��![]() �������У������ɺã��������ֿ�ʼ�Ǽۣ��Ǽۺ�ÿ����������ѧϰ���������ܴﵽ10580Ԫ�����ܣ�������Ƕ���Ԫ�������ܣ���˵�����ɣ�
�������У������ɺã��������ֿ�ʼ�Ǽۣ��Ǽۺ�ÿ����������ѧϰ���������ܴﵽ10580Ԫ�����ܣ�������Ƕ���Ԫ�������ܣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���BAC=90�㣬AB=AC��D��AC����һ���㣬CE��BD��E��

��1����ͼ��1������BDƽ����ABCʱ��������ECD�Ķ��������ӳ�CE��BA���ӳ����ڵ�F����ȫͼ�Σ�̽��BD��EC��������ϵ����֤����Ľ��ۣ�
��2����ͼ��2��������A��AF��BE�ڵ�F�������߶�BE��CE��AF֮���������ϵ����֤����IJ��룮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2019 �� 3 �� 31 �գ��Ͼ������µļ۸���ʽʵʩ��ʵ�������۽��Żݣ���ͨ����ÿ�³ֿ������������������ۼƽ����� 150 Ԫʱ��ÿ�γ���������Ʊ�۴� 9��5 �ۣ��������ۼƽ� ��� 150 Ԫʱ���ﵽ�涨�������ۼƽ�����ij˴Σ�Ʊ�������ۿ����±���ʾ��
�����ۼƽ�� | �ۿ� |
| 9�� |
| 8�� |
| 9.5�� |
С���ϡ��°�ÿ�γ����ĵ�������Ʊ��Ϊ 10Ԫ��2019�� 4�·����ϡ��°�ֿ��������� 40�Σ�
��1�������
��1 �� | ��2 �� | �� | ��15�� | ��16�� | ��17�� | �� | |
�����ۼ� ��Ԫ�� | 9.5 | 19 | �� | 142.5 | 152 | �� |
span>
��2��С�����µڼ��γ˳��������ۼƽ��� 20Ԫ������һԪһ�β���ʽ������⣩
��3��С�� 4�·��ϡ��°�ֿ����������������ۼƽ��Ϊ Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�DΪBC���е㣬DE��BC����BAC ��ƽ����AE��E��EF��AB��F��EG��AC��AC�ӳ�����G. AB=6, AC=3,��BF �ij�.
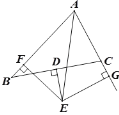
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У�AB��6����һ��ƽ�Ƴ�����ABCD��AB�ķ�������ƽ��5����λ���ȣ��õ�������A1B1C1D1����2��ƽ�Ƴ�����A1B1C1D1��A1B1�ķ�������ƽ��5����λ���ȣ��õ�������A2B2C2D2��������n��ƽ�Ƴ�����An��1Bn��1Cn��1Dn��1��An��1Bn��1�ķ�������ƽ��5����λ���ȣ��õ�������AnBnCnDn��n��2������ABn�ij���Ϊ2 026����n��ֵΪ�� ����
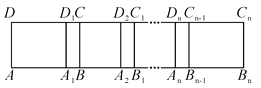
A. 407B. 406C. 405D. 404
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������y��ax![]() +bx+c��ͼ��������ƽ��3����λ��������ƽ��2����λ�����õ�ͼ��Ľ���ʽ��y��x
+bx+c��ͼ��������ƽ��3����λ��������ƽ��2����λ�����õ�ͼ��Ľ���ʽ��y��x![]() ��3x+5����a+b+c=__________��
��3x+5����a+b+c=__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���η���x2��2x+m��1=0������ʵ����x1��x2��
��1����m��ȡֵ��Χ��
��2����x12+x22=6x1x2ʱ����m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��PM2.5��ָ�����ڿ����еĿ�������ѧ����ֱ��С�ڻ����2.5�Ŀ����Ҳ��Ϊ����ο��������PM2.5������Ŀ��������±����ӵ�����2013��ȫ��ÿ���PM2.5�վ�ֵ��ֵ����λ����/�����ף��������������س�ȡ25���������Ϊ�����������ݼ�������������в�������Ƶ���ֲ���������ͼ��
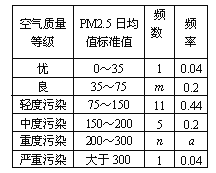
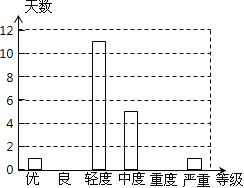
��1���������m��n��a��ֵ����������ͼ����������
��2������25���PM2.5�վ�ֵ�����Ƹ���Ŀ���������������Ƹ���(365��)��Լ�ж�����Ŀ��������ﵽ�Ż�����
��3��������ͼ������һ�����еĿ������������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com