
九(1)班数学课题学习小组,为了研究学习二次函数问题,他们经历了实践一应用——探究的过程:
(1)实践:他们对一条公路上横截面为抛物线的单向双车道的隧道(如图①)进行测量,测得一隧道的路面宽为10 m.隧道顶部最高处距地面6.25 m,并画出了隧道截面图.建立了如图②所示的直角坐标系.请你求出抛物线的解析式.

(2)应用:按规定机动车辆通过隧道时,车顶部与隧道顶部在竖直方向上的高度差至少为0.5 m.为了确保安全.问该隧道能否让最宽3 m.最高3.5 m的两辆厢式货车居中并列行驶(两车并列行驶时不考虑两车间的空隙)?
(3)探究:该课题学习小组为进一步探索抛物线的有关知识,他们借助上述抛物线模型塑.提出了以下两个问题,请予解答:
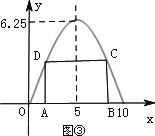
Ⅰ.如图③,在抛物线内作矩形ABCD,使顶点C、D落在抛物线上.顶点A、B落在x轴上.设矩形ABCD的周长为l,求l的最大值.
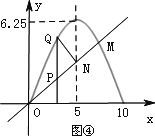
Ⅱ.如图④,过原点作一条y=x的直线OM,交抛物线于点M.交抛物线对称轴于点N,P为直线OM上一动点,过P点作x轴的垂线交抛物线于点Q.问在直线OM上是否存在点P,使以P、N、Q为顶点的三角形是等腰直角三角形?若存在,请求出P点的坐标;若不存在,请说明理由.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
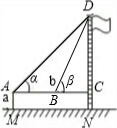
| 课题 | 测量校内旗杆高度 | ||
| 目的 | 运用所学数学知识及数学方法解决实际问题---测量旗杆高度 | ||
| 方案 | 方案一 | 方案二 | 方案三 |
示意图 |
 |
 |
|
| 测量工具 | 皮尺、测角仪 | 皮尺、测角仪 | |
| 测量数据 | AM=1.5m,AB=10m ∠α=30°,∠β=60° |
AM=1.5m,AB=20m ∠α=30°,∠β=60° |
|
| 计算过程(结 果保留根号) |
解: | 解: | |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 课题 | 测量校内旗杆高度 | ||
| 目的 | 运用所学数学知识及数学方法解决实际问题----测量旗杆高度 | ||
| 方案 | 方案一 | 方案二 | 方案三 |
示意图 |
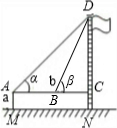 |
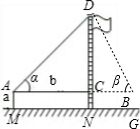 |
|
| 测量工具 | 皮尺、测角仪 | 皮尺、测角仪 | |
| 测量数据 | AM=1.5m,AB=10m ∠α=30°,∠β=60° |
AM=1.5m,AB=20m ∠α=30°,∠β=60° |
|
| 计算过程(结 果保留根号) |
解: |
解: | |
查看答案和解析>>
科目:初中数学 来源: 题型:
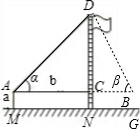
| 课题 | 测量校内旗杆高度 |
| 目的 | 运用所学数学知识及数学方法解决实际问题--测量旗杆高度 |
| 示意图 | 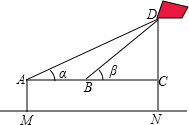 |
| 测量工具 | 皮尺、测角仪 |
| 测量数据: | AM=1.5m,AB=10m,∠α=30°,∠β=60° |
| 计算过程(结 果保留根号) |
解: |
| 测量结果 | DN= |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 课题 | 测量校内旗杆高度 | ||
| 目的 | 运用所学数学知识及数学方法解决实际问题----测量旗杆高度 | ||
| 方案 | 方案一 | 方案二 | 方案三 |
示意图 |  |  | |
| 测量工具 | 皮尺、测角仪 | 皮尺、测角仪 | |
| 测量数据 | AM=1.5m,AB=10m ∠α=30°,∠β=60° | AM=1.5m,AB=20m ∠α=30°,∠β=60° | |
| 计算过程(结 果保留根号) | 解: | 解: | |
查看答案和解析>>
科目:初中数学 来源:第1章《解直角三角形》中考题集(35):1.5 解直角三角形的应用(解析版) 题型:解答题
| 课题 | 测量校内旗杆高度 | ||
| 目的 | 运用所学数学知识及数学方法解决实际问题---测量旗杆高度 | ||
| 方案 | 方案一 | 方案二 | 方案三 |
示意图 | 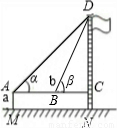 | 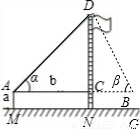 | |
| 测量工具 | 皮尺、测角仪 | 皮尺、测角仪 | |
| 测量数据 | AM=1.5m,AB=10m ∠α=30°,∠β=60° | AM=1.5m,AB=20m ∠α=30°,∠β=60° | |
| 计算过程(结 果保留根号) | 解: | 解: | |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com