
 如图,用细线悬挂一个小球,小球在竖直平面内的A、C两点间来回摆动,A点与地面距离AN=14cm,小球在最低点B时,与地面距离BM=5cm,∠AOB=66°,求细线OB的长度.(参考数据:sin66°≈0.91,cos66°≈0.40,tan66°≈2.25)
如图,用细线悬挂一个小球,小球在竖直平面内的A、C两点间来回摆动,A点与地面距离AN=14cm,小球在最低点B时,与地面距离BM=5cm,∠AOB=66°,求细线OB的长度.(参考数据:sin66°≈0.91,cos66°≈0.40,tan66°≈2.25) 分析 设细线OB的长度为xcm,作AD⊥OB于D,证出四边形ANMD是矩形,得出AN=DM=14cm,求出OD=x-9,在Rt△AOD中,由三角函数得出方程,解方程即可.
解答 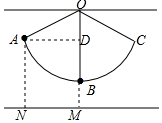 解:设细线OB的长度为xcm,作AD⊥OB于D,如图所示:
解:设细线OB的长度为xcm,作AD⊥OB于D,如图所示:
∴∠ADM=90°,
∵∠ANM=∠DMN=90°,
∴四边形ANMD是矩形,
∴AN=DM=14cm,
∴DB=14-5=9cm,
∴OD=x-9,
在Rt△AOD中,cos∠AOD=$\frac{OD}{AO}$,
∴cos66°=$\frac{x-9}{x}$=0.40,
解得:x=15,
∴OB=15cm.
点评 本题考查解直角三角形的应用,解此题关键是把实际问题转化为数学问题,本题只要把实际问题抽象到三角形中,根据线段之间的转换列方程即可.注意实际问题要入进.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 第1次 | 第2次 | 第3次 | 第4次 | 第5次 | 平均成绩 | |
| 甲 | 7 | ▲ | 8 | 10 | 8 | 8 |
| 乙 | 7 | 8 | 8 | 9 | 8 | ▲ |
| A. | 甲运动员的第2次射击成绩为7环 | B. | 乙运动员的平均射击成绩为8环 | ||
| C. | 甲运动员这5次射击成绩的方差为6 | D. | 乙运动员的成绩更稳定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
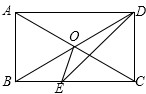 如图,在四边形ABCD中,AD∥BC,∠ABC=∠ADC=90°,对角线AC,BD交于点O,DE平分∠ADC交BC于点E,连接OE.
如图,在四边形ABCD中,AD∥BC,∠ABC=∠ADC=90°,对角线AC,BD交于点O,DE平分∠ADC交BC于点E,连接OE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com