
【题目】如图所示,AB是⊙O直径,OD⊥弦BC于点F,且交⊙O于点E,若∠AEC=∠ODB. 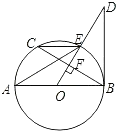
(1)判断直线BD和⊙O的位置关系,并给出证明;
(2)当AB=10,BC=8时,求BD的长.
【答案】
(1)解:直线BD和⊙O相切
证明:∵∠AEC=∠ODB,∠AEC=∠ABC
∴∠ABC=∠ODB
∵OD⊥BC
∴∠DBC+∠ODB=90°
∴∠DBC+∠ABC=90°
∴∠DBO=90°
∴直线BD和⊙O相切
(2)解:连接AC
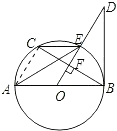
∵AB是直径
∴∠ACB=90°
在Rt△ABC中,AB=10,BC=8
∴ ![]()
∵直径AB=10
∴OB=5.
由(1),BD和⊙O相切
∴∠OBD=90°
∴∠ACB=∠OBD=90°
由(1)得∠ABC=∠ODB,
∴△ABC∽△ODB
∴ ![]()
∴ ![]() ,解得BD=
,解得BD= ![]() .
.
【解析】(1)因为同弧所对的圆周角相等,所以有∠AEC=∠ABC,又∠AEC=∠ODB,所以∠ABC=∠ODB,OD⊥弦BC,即∠ABC+∠BOD=90°,则有∠ODB+∠BOD=90°,即BD垂直于AB,所以BD为切线.(2)连接AC,由于AB为直径,所以AC和BC垂直,又由(1)知∠ABC=∠ODB,所以有△ACB∽△OBD,而AC可由勾股定理求出,所以根据对应线段成比例求出BD.
【考点精析】本题主要考查了勾股定理的概念和圆周角定理的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半才能正确解答此题.


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案科目:初中数学 来源: 题型:
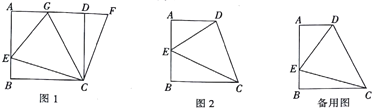
【题目】如图1,在正方形ABCD中,点E是AB上一点,点F是AD延长线上一点,且DF=BE,连接CE、CF.
(1)求证:CE=CF.
(2)在图1中,若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?
(3)根据你所学的知识,运用(1)、(2)解答中积累的经验,完成下列各题,如图2,在四边形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC,且∠DCE=45°.
①若AE=6,DE=10,求AB的长;
②若AB=BC=9,BE=3,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
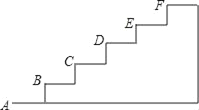
【题目】如图是某台阶的一部分,如果A点的坐标为(0,0),B点的坐标为(1,1),
(1)请建立适当的直角坐标系,并写出其余各点的坐标;
(2)如果台阶有10级,请你求出该台阶的长度和高度;
(3)若这10级台阶的宽度都是2m,单位长度为1m,现要将这些台阶铺上地毯,需要多少平方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解嘉峪关初三学生体育测试自选项目的情况,从我市初三学生中随机抽取中部分学生的自选项目进行统计,绘制了扇形统计图和频数分布直方图,请根据图中信息,回答下列问题: 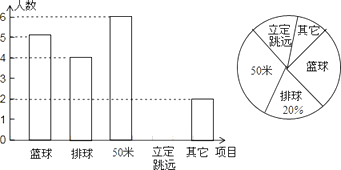
(1)本次调查共抽取了名学生;
(2)此次调查报其他项目的人数占了(填百分数),报立定跳远的人数是;
(3)扇形统计图中50米部分所对应的圆心角的度数是;
(4)我市共有初三学生3000名,估计我市有多少名学生选报篮球项目?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了加强公民的节水意识,合理利用水资源,各地采用价格调控手段达到节约用水的目的,某市规定如下用水收费标准:每户每月的用水量不超过6立方米时,水费按每立方米a元收费,超过6立方米时,不超过的部分每立方米仍按a元收费,超过的部分每立方米按c元收费,该市某户今年9、10月份的用水量和所交水费如下表所示:
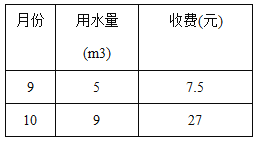
设某户每月用水量x(立方米),应交水费y(元)
(1)a= ,c=
(2)当x≤6,x≥6时,分别求出y于x的函数关系式
(3)若该户11月份用水量为8立方米,求该户11 月份水费是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,将两个正方形(每个角都是![]() )的一个顶点重合放置,若
)的一个顶点重合放置,若![]() ,求
,求![]() 的度数;
的度数;
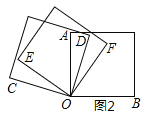
(2)如图2,将三个正方形的一个顶点重合放置,若![]() ,求
,求![]() 的度数;
的度数;
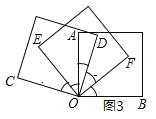
(3)如图3,将三个正方形的一个顶点重合放置,若![]() 平分
平分![]() ,那么
,那么![]() 平分
平分![]() 吗?为什么?
吗?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知二次函数y=ax2+bx+c(a≠0)的图象的顶点P的横坐标是4,图象交x轴于点A(m,0)和点B,且m>4,那么AB的长是( ) 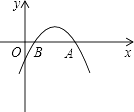
A.4+m
B.m
C.2m﹣8
D.8﹣2m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2﹣2x+3与x轴交于点A,B,把抛物线与线段AB围成的图形记为C1 , 将Cl绕点B中心对称变换得C2 , C2与x轴交于另一点C,将C2绕点C中心对称变换得C3 , 连接C,与C3的顶点,则图中阴影部分的面积为( ) 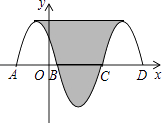
A.32
B.24
C.36
D.48
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com