”–AΓΔBΓΔCΓΔDΓΔE 5ΈΜΆ§―ß“ά¥Έ’Ψ‘ΎΡ≥‘≤÷ή…œΘ§ΟΩ»Υ ÷…œΖ÷±πΡΟ”––ΓΤλ16ΓΔ8ΓΔ12ΓΔ4ΓΔ15ΟφΘ§œ÷“Σ ΙΟΩ»Υ ÷÷–ΒΡ–ΓΤλ ΐœύΒ»Θ°“Σ«σœύΝΎΒΡΆ§―ß÷°ΦδœύΜΞΒς’ϊΘ®≤ΜœύΝΎΒΡ≤ΜΉςœύΜΞΒς’ϊΘ©Θ§…ηAΗχB”–x1ΟφΘ®x1ΘΨ0 ±Φ¥ΈΣAΗχB”–x1ΟφΘΜx1ΘΦO ±Φ¥ΈΣBΗχA”–x1ΟφΘ°“‘œ¬Ά§Θ©Θ§BΗχC”–x2ΟφΘΚCΗχD”–x3ΟφΘ§DΗχE”–x4ΟφΘ§EΗχA”–x5ΟφΘ§Έ x1ΓΔx2ΓΔx3ΓΔx4ΓΔx5Ζ÷±πΈΣΕύ…Ό ±≤≈Ρή ΙΒςΕ·ΒΡ–ΓΤλΉή ΐ|x1|+|x2|+|x3|+|x4|+|x5|Ήν–ΓΘΩ
ΓΨ¥πΑΗΓΩ
Ζ÷ΈωΘΚΗυΨίΧβ“βΝ–≥ωΖΫ≥ΧΉιΘ§Α―“ΜΗωΈ¥÷Σ ΐΒ±Ής“―÷ΣΘ§±μ Ψ≥ωΤδ”ύΒΡΈ¥÷Σ ΐΘ§ΗυΨίΧβ“β»ΓΤδΨχΕ‘÷ΒΘ§Μ≠≥ω ΐ÷αΘ§’“≥ωΗςΕ‘”ΠΒψΘ§«σ≥ωΤδΉν–Γ÷ΒΘ°
Ϋβ¥πΘΚΫβΘΚ”…”ΎΙ≤”––ΓΤλΟφ ΐΈΣ16+8+12+4+15=55ΟφΘ§“Σ ΙΟΩ»Υ ÷÷–ΒΡ–ΓΤλΟφ ΐœύΒ»Θ§ΟΩ»ΥΨυΈΣ11ΟφΘ°
”…Χβ“βΘΚ

Θ§
±δ–ΈΒΟΘΚ

Θ§
Γύ|x
1|+|x
2|+|x
3|+x
4|+|x
5|=|x
2+3|+|x
2|+|x
2+1|+|x
2-6|+|x
2-2|=|x
2+3|+|x
2+1|+|x
2|+|x
2-2|+|x
2-6|Θ§
…η Β ΐx
2‘Ύ ΐ÷α…œΒΡΕ‘”ΠΒψΈΣPΘ§

Β ΐ-3Θ§-1Θ§0Θ§2Θ§6‘Ύ ΐ÷α…œΒΡΕ‘”ΠΒψΖ÷±πΈΣP
1Θ§P
2Θ§P
3Θ§P
4Θ§P
5Θ§
Γύ|x
1|+|x
2|+|x
3|+x
4|+|x
5|=|PP
1|+|PP
2|+|PP
3|+|PP
4|+|PP
5|Θ§
Β±«“ΫωΒ±P‘ΎœΏΕΈP
1P
5…œ ±|PP
1|+|PP
5|”–Ήν–Γ÷Β9Θ§
Β±«“ΫωΒ±P‘ΎœΏΕΈP
2P
4…œ ±|PP
2|+|PP
4|”–Ήν–Γ÷Β3Θ§
Β±«“ΫωΒ±P”κΒψP
3÷ΊΚœ ±|PP
3|”–Ήν–Γ÷Β0Θ§
Φ¥Β±«“ΫωΒ±P”κΒψP
3÷ΊΚœΘ®x
2=0Θ© ±Θ§
x
1+x
2+x
3+x
4+x
5=|PP
1|+|PP
2|+|PP
3|+|PP
4|+|PP
5|”–Ήν–Γ÷Β12Θ°
Β±x
1=3Θ§x
2=0Θ§x
3=1Θ§x
4=-6Θ§x
5=-2 ±|x
1|+|x
2|+|x
3|+|x
4|+|x
5|”–Ήν–Γ÷Β12Θ°
ΒψΤάΘΚ¥ΥΧβ±»ΫœΗ¥‘”Θ§…φΦΑΒΫΥΡ‘Σ“Μ¥ΈΖΫ≥ΧΉιΦΑΨχΕ‘÷ΒΒΡœύΙΊ÷Σ ΕΘ§Ϋβ¥π¥ΥάύΧβΡΩΒΡΙΊΦϋ «Μ≠≥ω ΐ÷αΘ§ΗυΨί ΐ–ΈΫαΚœΫβΧβΘ°

 Θ§
Θ§ Θ§
Θ§



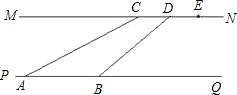 »γΆΦΘ§Κ”ΝςΒΡΝΫΑΕPQΓΔMNΜΞœύΤΫ––Θ§Κ”ΑΕMN…œ”–“Μ≈≈ΦδΗτΈΣ50ΟΉΒΡΒγœΏΗΥCΓΔDΓΔEΓ≠Θ§Ρ≥»Υ‘ΎΚ”ΑΕPQΒΡA¥Π≤βΒΟΓœCAQ=30ΓψΘ§»ΜΚσ―ΊΚ”ΑΕΉΏΝΥ110ΟΉΒΫ¥οB¥ΠΘ§≤βΒΟΓœDBQ=45ΓψΘ§«σΚ”ΝςΒΡΩμΕ»Θ°
»γΆΦΘ§Κ”ΝςΒΡΝΫΑΕPQΓΔMNΜΞœύΤΫ––Θ§Κ”ΑΕMN…œ”–“Μ≈≈ΦδΗτΈΣ50ΟΉΒΡΒγœΏΗΥCΓΔDΓΔEΓ≠Θ§Ρ≥»Υ‘ΎΚ”ΑΕPQΒΡA¥Π≤βΒΟΓœCAQ=30ΓψΘ§»ΜΚσ―ΊΚ”ΑΕΉΏΝΥ110ΟΉΒΫ¥οB¥ΠΘ§≤βΒΟΓœDBQ=45ΓψΘ§«σΚ”ΝςΒΡΩμΕ»Θ°