
解:(1)在△MBC中,∠MCB=90°,BC=2,
又∵M是边AC的中点,
∴AM=MC=

BC=1,(1分)
∴MB=
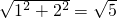
,(1分)
又CH⊥BM于H,则∠MHC=90°,
∴∠MCH=∠MBC,(1分)
∴sin∠MCH=
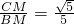
.(1分)
(2)在△MHC中,
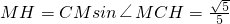
.(1分)
∴AM
2=MC
2=MH•MB,
即
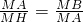
,(2分)
又∵∠AMH=∠BMA,
∴△AMH∽△BMA,(1分)
∴∠ABM=∠CAH.(1分)
(3)∵△AMH∽△BMA,
∴
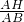
=
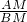
,
在Rt△BMC中,BM=

=

,
在Rt△ABC中,AB=

AC=2

,
∴AH=
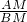
×AB=
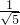
×2

=

,
∵∠ABM=∠CAH,∠BAC=∠ABC=45°,
∴∠HAD=∠MCH,
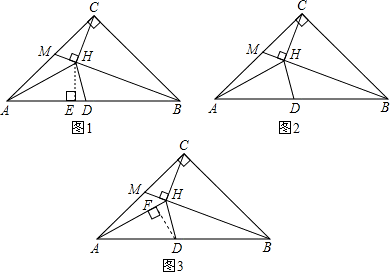
①AD为底边时,如图1,AD=2AHcos∠HAD,
∵sin∠MCH=

,
∴cos∠HAD=
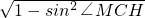
=

,
∴AD=2×

×

=
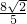
;
②HD为底边时,如图2,AD=AH=

;
③AH为底边时,AD=

AH÷cos∠HAD=

×

÷

=

×
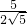
=

.
故AD的长为:
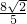
,

或

.
分析:(1)根据已知条件“M是边AC的中点”知AM=MC=1;在直角三角形MBC中利用勾股定理求得MB=

,由∠HCB+∠HBC=∠CMH+∠MCH=90°求得∠MCH=∠MBC;所以sin∠MCH=
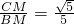
;
(2)在Rt△MHC中,利用边角关系求得MH的值,再在Rt△CBM中利用射影定理求得
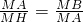
;然后根据SAS判定△AMH∽△BMA;最后由相似三角形的对应角相等证明∠ABM=∠CAH;
(3)分三种情况讨论:①AD为底边时,AD的长度;②HD为底边时,AD的长度;③AH为底边时,AD的长度.
点评:本题考查了相似三角形的判定与性质、等腰三角形的判定及勾股定理的应用.解答(3)题时,注意要分三种情况来求AD的长度,即:①AD为底边时;②AH为底边时;③HD为底边时.以防漏解.

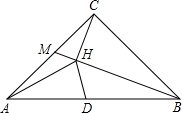 如图,在△ABC中,∠ACB=90°,AC=BC=2,M是边AC的中点,CH⊥BM于H.
如图,在△ABC中,∠ACB=90°,AC=BC=2,M是边AC的中点,CH⊥BM于H. 解:(1)在△MBC中,∠MCB=90°,BC=2,
解:(1)在△MBC中,∠MCB=90°,BC=2, BC=1,(1分)
BC=1,(1分)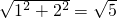 ,(1分)
,(1分)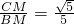 .(1分)
.(1分)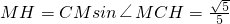 .(1分)
.(1分)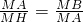 ,(2分)
,(2分)
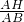 =
=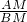 ,
, =
= ,
, AC=2
AC=2 ,
,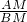 ×AB=
×AB=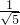 ×2
×2 =
= ,
, ,
,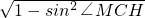 =
= ,
, ×
× =
=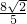 ;
; ;
; AH÷cos∠HAD=
AH÷cos∠HAD= ×
× ÷
÷ =
= ×
×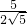 =
= .
.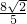 ,
, 或
或 .
. ,由∠HCB+∠HBC=∠CMH+∠MCH=90°求得∠MCH=∠MBC;所以sin∠MCH=
,由∠HCB+∠HBC=∠CMH+∠MCH=90°求得∠MCH=∠MBC;所以sin∠MCH=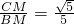 ;
;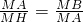 ;然后根据SAS判定△AMH∽△BMA;最后由相似三角形的对应角相等证明∠ABM=∠CAH;
;然后根据SAS判定△AMH∽△BMA;最后由相似三角形的对应角相等证明∠ABM=∠CAH;

 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为