
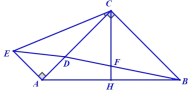
【题目】如图,禁止捕鱼期间,某海上稽查队在某海域巡逻,上午某一时刻在A处接到指挥部通知,在他们东北方向距离12海里的B处有一艘捕鱼船,正在沿南偏东75°方向以每小时10海里的速度航行,稽查队员立即乘坐巡逻船以每小时14海里的速度沿北偏东某一方向出发,在C处成功拦截捕鱼船,求巡逻船从出发到成功拦截捕鱼船所用的时间.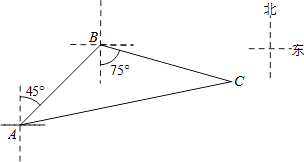
【答案】解:设巡逻船从出发到成功拦截所用时间为x小时;如图所示,
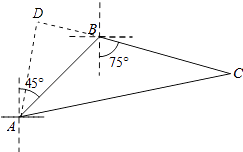
由题意得:∠ABC=45°+75°=120°,AB=12,BC=10x,AC=14x,
过点A作AD⊥CB的延长线于点D,
在Rt△ABD中,AB=12,∠ABD=45°+(90°﹣75°)=60°,
∴BD=ABcos60°= ![]() AB=6,AD=ABsin60°=6
AB=6,AD=ABsin60°=6 ![]() ,
,
∴CD=10x+6.
在Rt△ACD中,由勾股定理得: ![]() ,
,
解得: ![]() (不合题意舍去).
(不合题意舍去).
答:巡逻船从出发到成功拦截所用时间为2小时.
【解析】根据题意,添加辅助线过点A作AD⊥CB的延长线于点D,易求得∠ABC的度数,在Rt△ABD中,由解直角三角形求出BD,AD的长度,表示出CD的长,在Rt△ACD中,由勾股定理列出方程求解即可。
【考点精析】本题主要考查了勾股定理的概念和解直角三角形的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法)才能正确解答此题.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】张老师抽取了九年级部分男生掷实心球的成绩进行整理,分成5个小组(x表示成绩,单位:米).A组:5.25≤x<6.25;B组:6.25≤x<7.25;C组:7.25≤x<8.25;D组:8.25≤x<9.25;E组:9.25≤x<10.25,规定x≥6.25为合格,x≥9.25为优秀.并绘制出扇形统计图和频数分布直方图(不完整).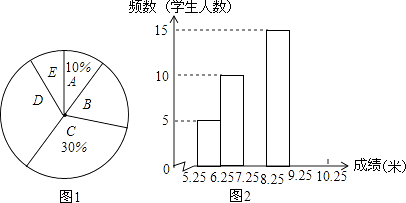
(1)抽取的这部分男生有人,请补全频数分布直方图;
(2)抽取的这部分男生成绩的中位数落在组?扇形统计图中D组对应的圆心角是多少度?
(3)如果九年级有男生400人,请你估计他们掷实心球的成绩达到合格的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在平面直角坐标系xOy中的位置如图所示.

(1)作△ABC关于点C成中心对称的△A1B1C1.
(2)将△A1B1C1向右平移4个单位,作出平移后的△A2B2C2.
(3)在x轴上求作一点P,使PA1+PC2的值最小,并写出点P的坐标(不写解答过程,直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,三角形纸片ABC中,∠A=65°,∠B=75°,将∠C沿DE对折,使点C落在ΔABC外的点![]() 处,若∠1=20°,则∠2的度数为( )
处,若∠1=20°,则∠2的度数为( )

A. 80°B. 90°
C. 100°D. 110°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC纸片中,∠C=90°,AC=6,BC=8,点D在边BC 上,以AD为折痕将△ABD折叠得到△AB′D,AB′与边BC交于点E.若△DEB′为直角三角形,则BD的长是_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
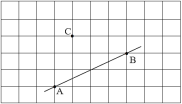
【题目】(1)过点C画AB的平行线CD;
(2)过点C画AB的垂线,垂足为E;
(3)线段CE的长度是点C到直线__________的距离;
(4)连接CA、CB,在线段CA、CB、CE中,线段__________最短,理由:______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=BC,CH为△ABC斜边上的中线,点F为CH上一点,连接BF并延长交AC于点D,过点A作AE⊥AC,连接CE和DE,若∠ACE=2∠ABF,CE=13,CD=8,则△CDE的面积为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com