
分析 (1)方程整理后,利用平方根定义开方即可求出解;
(2)方程整理后,利用立方根定义开立方即可求出解;
(3)方程组利用加减消元法求出解即可.
解答 解:(1)方程整理得:(x-2)2=9,
开方得:x-2=3或x-2=-3,
解得:x=5或x=-1;
(2)方程整理得:(x-1)3=-8,
开立方得:x-1=-2,
解得:x=-1;
(3)$\left\{\begin{array}{l}{x+2y=5①}\\{2x-7y=-12②}\end{array}\right.$,
①×2-②得:11y=22,
解得:y=2,
把y=2代入①得:x=1,
则方程组的解为$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点A是射线OX上一点,OA=4,过A作AB⊥OX,且AB=2,连结OB,作∠XOY=∠ABO,过B任作一直线m,分别交射线AX,射线OY于C,D两点,设$\frac{BC}{CD}$=$\frac{1}{k}$
如图,点A是射线OX上一点,OA=4,过A作AB⊥OX,且AB=2,连结OB,作∠XOY=∠ABO,过B任作一直线m,分别交射线AX,射线OY于C,D两点,设$\frac{BC}{CD}$=$\frac{1}{k}$查看答案和解析>>
科目:初中数学 来源: 题型:解答题
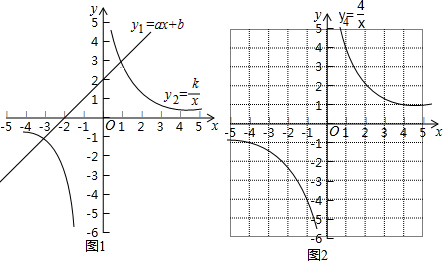
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,抛物线y=ax2+bx-2经过点A(1,0)和点B(4,0),与y轴交于点C.
如图,抛物线y=ax2+bx-2经过点A(1,0)和点B(4,0),与y轴交于点C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com