
【题目】如图,AB是⊙O直径,点C在⊙O上,AD平分∠CAB,BD是⊙O的切线,AD与BC相交于点E. 
(1)求证:BD=BE;
(2)若DE=2,BD= ![]() ,求CE的长.
,求CE的长.
【答案】
(1)解:设∠BAD=α,
∵AD平分∠BAC
∴∠CAD=∠BAD=α,
∵AB是⊙O的直径,∴∠ACB=90°,
∴∠ABC=90°﹣2α,
∵BD是⊙O的切线,
∴BD⊥AB,
∴∠DBE=2α,
∠BED=∠BAD+∠ABC=90°﹣α,
∴∠D=180°﹣∠DBE﹣∠BED=90°﹣α,
∴∠D=∠BED,
∴BD=BE
(2)解:设AD交⊙O于点F,CE=x,则AC=2x,连接BF,
∵AB是⊙O的直径,
∴∠AFB=90°,
∵BD=BE,DE=2,
∴FE=FD=1,
∵BD= ![]() ,
,
∴tanα= ![]() ,
,
∴AB= ![]() =2
=2 ![]()
在Rt△ABC中,
由勾股定理可知:(2x)2+(x+ ![]() )2=(2
)2=(2 ![]() )2,
)2,
∴解得:x=﹣ ![]() 或x=
或x= ![]() ,
,
∴CE= ![]() ;
;

【解析】(1))设∠BAD=α,由于AD平分∠BAC,所以∠CAD=∠BAD=α,进而求出∠D=∠BED=90°﹣α,从而可知BD=BE;(2)设CE=x,由于AB是⊙O的直径,∠AFB=90°,又因为BD=BE,DE=2,FE=FD=1,由于BD= ![]() ,所以tanα=
,所以tanα= ![]() ,从而可求出AB=
,从而可求出AB= ![]() =2
=2 ![]() ,利用勾股定理列出方程即可求出x的值.
,利用勾股定理列出方程即可求出x的值.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】已知某开发区有一块四边形的空地![]() ,如图所示,现计划在空地上种植草皮,经测量
,如图所示,现计划在空地上种植草皮,经测量![]() ,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草皮需要200元,问要多少投入?
,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草皮需要200元,问要多少投入?

查看答案和解析>>
科目:初中数学 来源: 题型:
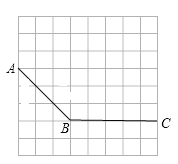
【题目】作图题:(只保留作图痕迹)如图,在方格纸中,有两条线段AB、BC.利用方格纸完成以下操作:
(1)过点A作BC的平行线;
(2)过点C作AB的平行线,与(1)中的平行线交于点D;
(3)过点B作AB的垂线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一个不定的正方形ABCD,它的两个相对的顶点A,C分别在边长为1的正六边形一组对边上,另外两个顶点B,D在正六边形内部(包括边界),则正方形边长a的取值范围是
查看答案和解析>>
科目:初中数学 来源: 题型:
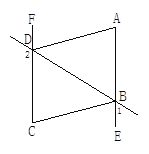
【题目】如图,∠1+∠2=180°,∠DAE=∠BCF,DA平分∠BDF.
(1)AE与FC会平行吗?说明理由.
(2)AD与BC的位置关系如何?为什么?
(3)BC平分∠DBE吗?为什么.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B两点在数轴上对应的数是a和b,且![]() ,点P为数轴上一动点,对应的数为x.
,点P为数轴上一动点,对应的数为x.
(1)求A、B两点间的距离;
(2)是否存在点P,使AP=![]() PB,若存在,求出x的值;若不存在,说明理由.
PB,若存在,求出x的值;若不存在,说明理由.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列定义一种关于n的运算:①当n是奇数时,结果为3n+5 ②n为偶数时结果是![]() (其中k是使
(其中k是使![]() 是奇数的正整数),并且运算重复进行.例如:取n=26,则…,若n=449,则第449次运算结果是( )
是奇数的正整数),并且运算重复进行.例如:取n=26,则…,若n=449,则第449次运算结果是( )
A. 1 B. 2 C. 7 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了美化校园计划购买茶花、桂花两种树苗共600株,茶花树苗每株35元,桂花树苗每株40元.相关资料表明:茶花、桂花树苗的成活率分别为80%,90%.
(1)若购买这两种树苗共用去22000元,则茶花、桂花树苗各购买多少株?
(2)若要使这批树苗的总成活率不低于85%,则茶花树苗至多购买多少株?
(3)在(2)的条件下,应如何选购树苗,使购买树苗的费用最低,并求出最低费用.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com