
����Ŀ��ijУΪ������У�ƻ�����軨�����������繲600�꣬�軨����ÿ��35Ԫ��������ÿ��40Ԫ��������ϱ������軨��������ijɻ��ʷֱ�Ϊ80%��90%��
��1�����������������繲��ȥ22000Ԫ����軨�����������������ꣿ
��2����Ҫʹ����������ܳɻ��ʲ�����85%����軨�������������ꣿ
��3���ڣ�2���������£�Ӧ���ѡ�����磬ʹ��������ķ�����ͣ��������ͷ��ã�
���𰸡�
��1���⣺�蹺��軨����x�꣬������y�꣬����ɵã�
![]() ��
��
��� ![]() ��
��
�𣺹���軨����400�꣬������200�꣮
��2���⣺�蹺��軨����z�꣬�����磨600��z���꣬����ɵã�
80%z+90%��600��z����85%��600��
���z��300��
�𣺲軨���������300�꣮
��3���⣺����軨���繺��m�꣬��������ķ���ΪWԪ������ɵã�
W=35m+40��600��m��=��5m+24000
�ߩ�5��0��
��W��m�����������
��0��m��300��
�൱m=300ʱ��W����Сֵ��W=24000��5��300=22500Ԫ��
�𣺵�ѡ����軨����300�꣬������300��ʱ���ܷ������Ϊ22500Ԫ��
����������1���蹺��軨����x�꣬������y�꣬��������ɵ�һ����Ԫһ�η����飬��֮���ɵó���.
��2���蹺��軨����z�꣬�����磨600��z���꣬��������ɵ�һԪһ�β���ʽ���̣���֮���ɵó���.
��3������軨���繺��m�꣬��������ķ���ΪWԪ����������ɵ�W=35m+40��600��m��=��5m+24000���ٸ���һ�κ��������ʩ�5��0��W��m���������С�����Ա�����ȡֵ��Χ��0��m��300���ó�Wmin.


 ��ڽ��ȫ������ϵ�д�
��ڽ��ȫ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�Oֱ������C�ڡ�O�ϣ�ADƽ�֡�CAB��BD�ǡ�O�����ߣ�AD��BC�ཻ�ڵ�E�� 
��1����֤��BD=BE��
��2����DE=2��BD= ![]() ����CE�ij���
����CE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ֽ�ϵ�ÿ��С�����DZ߳�Ϊ1�������Σ����ǰ��Ը�������Ϊ�ߵ������γ�Ϊ����������Ρ���ͼ�еġ�ABC���Ǹ�������Σ��ڽ���ƽ��ֱ������ϵ��B������Ϊ����2����1����
��1���ѡ�ABC����ƽ��4���õ���A1B1C1��������A1B 1C1��д����A1�����ꣻ
��2���ѡ�ABC�Ƶ�C��˳ʱ����ת90���õ���A2B2C��������A2B2C��ͼ�β�д����A2�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ֱ�����ǰ��һ����Ƕ�����������ABCD�Ķ���A�غϣ��������ǰ��Ƶ�A��ת��ʹ���ǰ��и���ǵ������߷ֱ������ε�����BC��DC�ڵ�E��F������EF����EF=5��DF=2����BE�ij�Ϊ_______��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ֪��![]() ��ֱ��
��ֱ��![]() ��ֱ��
��ֱ��![]() ��
��![]() �ֱ��ཻ��C��D���㣮
�ֱ��ཻ��C��D���㣮
��1����ͼa����һ����P���߶�CD֮���˶�(����C��D�����غ�)�����ڵ�P���˶������У��Ƿ�ʼ�վ��С�3+��1=��2��һ��ϵ��Ϊʲô��
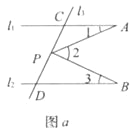
��2����ͼb��������P�߶�CD֮���˶�(����C��D�����غ�)�������������Ƿ����?������������д���µĽ��۲�˵�����ɣ�
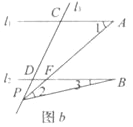
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������A(-3��-2)��B(2��-2)��C(3��1)��D(-2��1)�ĸ��㡣
��1���߶�AB��CD��ʲô��ϵ?
��2��˳������A��B��C��D�ĵ���ɵ�ͼ����ʲôͼ��?

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y=ax2+bx+c��a��0������ԭ�㣬����ΪA��h��k����h��0����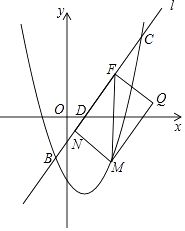
��1����h=1��k=2ʱ���������ߵĽ���ʽ��
��2����������y=tx2��t��0��Ҳ������A����a��t֮��Ĺ�ϵʽ��
��3���ڣ�2���������£���֪a=�� ![]() ��ֱ��l��y=
��ֱ��l��y= ![]() x��1��������y=tx2��
x��1��������y=tx2�� ![]() x��7���ڵ�B��C����x�ᣬy�ύ�ڵ�D��E����M��������y=tx2��
x��7���ڵ�B��C����x�ᣬy�ύ�ڵ�D��E����M��������y=tx2�� ![]() x��7�ϣ��ҵ�M�ĺ�����Ϊm��0��m��6����MF��y�ύ��ֱ��l�ڵ�F����N��ֱ��l�ϣ����ı���MNFQΪ���Σ���ͼ����������MNFQ���ܳ�ΪP����P�����ֵ��
x��7�ϣ��ҵ�M�ĺ�����Ϊm��0��m��6����MF��y�ύ��ֱ��l�ڵ�F����N��ֱ��l�ϣ����ı���MNFQΪ���Σ���ͼ����������MNFQ���ܳ�ΪP����P�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������:
(1)5a2b��![]() ��2ab2;
��2ab2;
(2)[(x+2y)2-(x+y)(x-y)-5y2]��2x;
(3)(-3.6��1010)��(-2��102)2;
(4)(2a-b+3)(2a-3+b).
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪AB��CD.

(1)��ͼ�٣�����ABE��30������BEC��148�������ECD�Ķ�����
(2)��ͼ�ڣ���CF��EB��CFƽ�֡�ECD����̽����ECD���ABE֮���������ϵ����֤����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com