
【题目】已知AB∥CD.

(1)如图①,若∠ABE=30°,∠BEC=148°,求∠ECD的度数;
(2)如图②,若CF∥EB,CF平分∠ECD,试探究∠ECD与∠ABE之间的数量关系,并证明.
【答案】(1)∠ECD=62°;(2)ABE=![]() ∠ECD,证明详见解析.
∠ECD,证明详见解析.
【解析】
(1)过点E作EF∥AB,根据平行线的性质即可得到∠ECD的度数;
(2)延长BE和DC相交于点G,利用平行线的性质、三角形的外角以及角平分线的性质即可得到答案.
(1)如图①,过点E作EF∥AB,
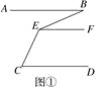
∵AB∥CD,
∴AB∥EF∥CD,
∴∠ABE=∠BEF,∠FEC+∠ECD=180°,
∵∠ABE=30°,∠BEC=148°,
∴∠FEC=118°,
∴∠ECD=180°-118°=62°.
(2)如图②,延长BE和DC相交于点G,
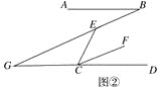
∵AB∥CD,
∴∠ABE=∠G,
∵BE∥CF,
∴∠GEC=∠ECF,
∵∠ECD=∠GEC+∠G,
∴∠ECD=∠ECF+∠ABE,
∵CF平分∠ECD,
∴∠ECF=∠DCF,
∴∠ECD=![]() ∠ECD+∠ABE,
∠ECD+∠ABE,
∴∠ABE=![]() ∠ECD.
∠ECD.


科目:初中数学 来源: 题型:
【题目】某校为了美化校园计划购买茶花、桂花两种树苗共600株,茶花树苗每株35元,桂花树苗每株40元.相关资料表明:茶花、桂花树苗的成活率分别为80%,90%.
(1)若购买这两种树苗共用去22000元,则茶花、桂花树苗各购买多少株?
(2)若要使这批树苗的总成活率不低于85%,则茶花树苗至多购买多少株?
(3)在(2)的条件下,应如何选购树苗,使购买树苗的费用最低,并求出最低费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是半圆直径,半径OC⊥AB于点O,D为半圆上一点,AC∥OD,AD与OC交于点E,连结CD、BD,给出以下三个结论:①OD平分∠COB;②BD=CD;③CD2=CECO,其中正确结论的序号是 . 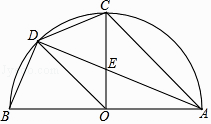
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在给定的一张平行四边形纸片上作一个菱形.甲、乙两人的作法如下:
甲:连接AC,作AC的垂直平分线MN分别交AD,AC,BC于M,O,N,连接AN,CM,则四边形ANCM是菱形.
乙:分别作∠A,∠B的平分线AE,BF,分别交BC,AD于E,F,连接EF,则四边形ABEF是菱形.
根据两人的作法可判断

A.甲正确,乙错误 B.乙正确,甲错误 C.甲、乙均正确 D.甲、乙均错误
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC的中线BD、CE相交于点O、M、N分别为OB、OC的中点.
(1)求证:MD和NE互相平分;
(2)若BD⊥AC,EM=2![]() ,OD+CD=7,求△OCB的面积.
,OD+CD=7,求△OCB的面积.
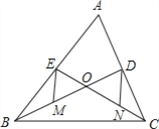
查看答案和解析>>
科目:初中数学 来源: 题型:
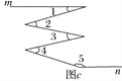
【题目】如图,在图a、图b、图c中都有直线m∥n,
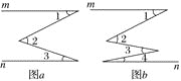
(1)在图a中,∠2和∠1、∠3之间的数量关系是__________________.
(2)猜想:在图b中,∠1、∠2、∠3、∠4之间的数量关系是____________________.
(3)猜想:在图c中,∠2、∠4和∠1、∠3、∠5的数量关系式是____________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分) 小丽想用一块面积为400cm2的正方形纸片,沿着边的方向裁处一块面积为300cm2的长方形纸片.(1)请帮小丽设计一种可行的裁剪方案;
(2)若使长方形的长宽之比为3:2,小丽能用这块纸片裁处符合要求的纸片吗?若能,请帮小丽设计一种裁剪方案,若不能,请简要说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com