
【题目】如图,在给定的一张平行四边形纸片上作一个菱形.甲、乙两人的作法如下:
甲:连接AC,作AC的垂直平分线MN分别交AD,AC,BC于M,O,N,连接AN,CM,则四边形ANCM是菱形.
乙:分别作∠A,∠B的平分线AE,BF,分别交BC,AD于E,F,连接EF,则四边形ABEF是菱形.
根据两人的作法可判断

A.甲正确,乙错误 B.乙正确,甲错误 C.甲、乙均正确 D.甲、乙均错误
【答案】C
【解析】
试题甲的作法正确:
∵四边形ABCD是平行四边形,∴AD∥BC。∴∠DAC=∠ACN。
∵MN是AC的垂直平分线,∴AO=CO。
在△AOM和△CON中,∵∠MAO=∠NCO,AO=CO,∠AOM=∠CON,
∴△AOM≌△CON(ASA),∴MO=NO。∴四边形ANCM是平行四边形。
∵AC⊥MN,∴四边形ANCM是菱形。
乙的作法正确:如图,
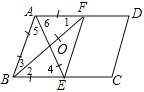
∵AD∥BC,∴∠1=∠2,∠6=∠4。
∵BF平分∠ABC,AE平分∠BAD,∴∠2=∠3,∠5=∠6。
∴∠1=∠3,∠5=∠4。∴AB=AF,AB=BE。∴AF=BE。
∵AF∥BE,且AF=BE,∴四边形ABEF是平行四边形。
∵AB=AF,∴平行四边形ABEF是菱形。
故选C。


科目:初中数学 来源: 题型:
【题目】如图,等腰直角三角板的一个锐角顶点与正方形ABCD的顶点A重合,将此三角板绕点A旋转,使三角板中该锐角的两条边分别交正方形的两边BC、DC于点E、F,连结EF.若EF=5,DF=2,则BE的长为_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)5a2b÷![]() ×2ab2;
×2ab2;
(2)[(x+2y)2-(x+y)(x-y)-5y2]÷2x;
(3)(-3.6×1010)÷(-2×102)2;
(4)(2a-b+3)(2a-3+b).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD相交于点O,下列条件中,不能说明AB⊥CD的是( )

A. ∠AOD=90°
B. ∠AOC=∠BOC
C. ∠BOC+∠BOD=180°
D. ∠AOC+∠BOD=180°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=x+1与反比例函数y= ![]() 的图象交于A,B两点,已知点A的坐标为(1,a),点B的坐标为(b,﹣1).
的图象交于A,B两点,已知点A的坐标为(1,a),点B的坐标为(b,﹣1).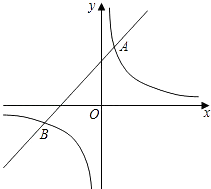
(1)求此反比例函数的解析式;
(2)当一次函数y=x+1的值大于反比例函数y= ![]() 的值时,求自变量x的取值范围.
的值时,求自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为预防甲型H1N1流感,某校对教室喷洒药物进行消毒.已知喷洒药物时每立方米空气中的含药量y(毫克)与时间x(分钟)成正比,药物喷洒完后,y与x成反比例(如图所示).现测得10分钟喷洒完后,空气中每立方米的含药量为8毫克.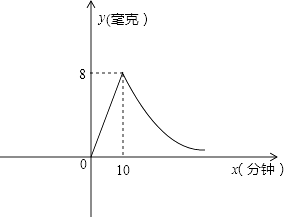
(1)求喷洒药物时和喷洒完后,y关于x的函数关系式;
(2)若空气中每立方米的含药量低于2毫克学生方可进教室,问消毒开始后至少要经过多少分钟,学生才能回到教室?
(3)如果空气中每立方米的含药量不低于4毫克,且持续时间不低于10分钟时,才能杀灭流感病毒,那么此次消毒是否有效?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB∥CD.

(1)如图①,若∠ABE=30°,∠BEC=148°,求∠ECD的度数;
(2)如图②,若CF∥EB,CF平分∠ECD,试探究∠ECD与∠ABE之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,![]() 、
、![]() 、
、![]() 三点的坐标分别为
三点的坐标分别为![]() 、
、![]() 、
、![]() .
.

(1)画出![]() ,则
,则![]() 的面积为_______;
的面积为_______;
(2)在![]() 中,点
中,点![]() 经过平移后的对应点为
经过平移后的对应点为![]() ,将
,将![]() 作同样的平移得到
作同样的平移得到![]() ,画出平移后的
,画出平移后的![]() ,并写出点
,并写出点![]() ,
,![]() 的坐标
的坐标![]() (_______);
(_______);![]() (_______);
(_______);
(3)![]() 为
为![]() 中一点,将点
中一点,将点![]() 向右平移4个单位,再向下平移6个单位得到点
向右平移4个单位,再向下平移6个单位得到点![]() ,则
,则![]() _______,
_______,![]() _______.
_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.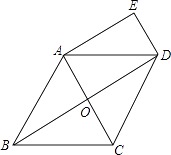
(1)求证:四边形AODE是矩形;
(2)若AB=6,∠BCD=120°,求四边形AODE的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com