
【题目】已知抛物线y=ax2+bx+c(a≠0)经过原点,顶点为A(h,k)(h≠0).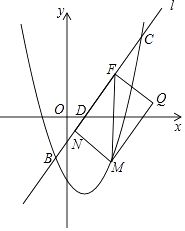
(1)当h=1,k=2时,求抛物线的解析式;
(2)若抛物线y=tx2(t≠0)也经过点A,过a与t之间的关系式;
(3)在(2)的条件下,已知a=﹣ ![]() ,直线l:y=
,直线l:y= ![]() x﹣1与抛物线y=tx2﹣
x﹣1与抛物线y=tx2﹣ ![]() x﹣7交于点B,C,与x轴,y轴交于点D,E,点M在抛物线y=tx2﹣
x﹣7交于点B,C,与x轴,y轴交于点D,E,点M在抛物线y=tx2﹣ ![]() x﹣7上,且点M的横坐标为m(0<m<6).MF∥y轴交于直线l于点F,点N在直线l上,且四边形MNFQ为矩形(如图),若矩形MNFQ的周长为P,求P的最大值.
x﹣7上,且点M的横坐标为m(0<m<6).MF∥y轴交于直线l于点F,点N在直线l上,且四边形MNFQ为矩形(如图),若矩形MNFQ的周长为P,求P的最大值.
【答案】
(1)解:∵由题意可知抛物线顶点坐标为(1,2),
∴可设抛物线解析式为y=a(x﹣1)2+2,
∵抛物线过原点,
∴0=a(0﹣1)2+2,解得a=﹣2,
∴抛物线解析式为y=﹣2(x﹣1)2+2;
(2)解:∵抛物线y=tx2(t≠0)也经过点A,
∴k=th2,
∴y=a(x﹣h)2+k=a(x﹣h)2+th2,
∵当x=0时y=0,
∴0=ah2+th2,
∵h≠0,
∴a+t=0,即a=﹣t;
(3)解:由(2)可知a=﹣t,
∴当a=-![]() 时,t=
时,t=![]() ,
,
∴M(m,![]() m2-
m2-![]() m-7),F(m,
m-7),F(m,![]() m﹣1),
m﹣1),
∴FM=(![]() m﹣1)﹣(
m﹣1)﹣(![]() m2﹣
m2﹣![]() m﹣7)=﹣
m﹣7)=﹣![]() m2+2m+6,
m2+2m+6,
又在y=![]() x﹣1中,
x﹣1中,
当x=0时,y=﹣1,y=0时,x=![]() ,
,
∴OD=![]() ,OE=1,
,OE=1,
∴DE=![]() =
=![]() ,
,
∵MF∥y轴,
∴∠DEO=∠MFN,
在矩形MNFQ中,NF=MF·cos∠MFN=MF·![]() =
=![]() MF,
MF,
MN=MF·sin∠MFN=MF·![]() =
=![]() MF,
MF,
∴P=2(MN+NF)=![]() MF=
MF=![]() (﹣
(﹣![]() m2+2m+6)=-
m2+2m+6)=-![]() m2+
m2+![]() m+
m+![]() =﹣
=﹣![]() (m﹣2)2+
(m﹣2)2+ ![]() ,
,
∵0<m<6,﹣![]() <0,
<0,
∴当m=2时,P取最大值,最大值为 ![]() .
.
【解析】(1)由题可知抛物线顶点坐标为(1,2),依此可设抛物线解析式为y=a(x﹣1)2+2,又抛物线过原点,从而得出抛物线解析式.
(2)将A点坐标代入抛物线y=tx2(t≠0),再将(0,0)代入y=a(x﹣h)2+k,由此即可得出即a=﹣t.
(3)由(2)知a=﹣t,由题意知M(m,![]() m2-
m2-![]() m-7),F(m,
m-7),F(m,![]() m﹣1),从而得FM=﹣
m﹣1),从而得FM=﹣![]() m2+2m+6;根据已知条件得OD=
m2+2m+6;根据已知条件得OD=![]() ,OE=1,
,OE=1,
根据勾股定理得DE=![]() ,由平行线性质得∠DEO=∠MFN;在矩形MNFQ中,由锐角三角函数定义得NF=
,由平行线性质得∠DEO=∠MFN;在矩形MNFQ中,由锐角三角函数定义得NF=![]() MF,MN=
MF,MN=![]() MF,从而得出P=2(MN+NF)=﹣
MF,从而得出P=2(MN+NF)=﹣![]() (m﹣2)2+
(m﹣2)2+ ![]() ,根据二次函数得性质和自变量的取值范围0<m<6得当m=2时,Pmin=
,根据二次函数得性质和自变量的取值范围0<m<6得当m=2时,Pmin= ![]() .
.
【考点精析】关于本题考查的勾股定理的概念和矩形的性质,需要了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;矩形的四个角都是直角,矩形的对角线相等才能得出正确答案.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,A、B两点在数轴上对应的数是a和b,且![]() ,点P为数轴上一动点,对应的数为x.
,点P为数轴上一动点,对应的数为x.
(1)求A、B两点间的距离;
(2)是否存在点P,使AP=![]() PB,若存在,求出x的值;若不存在,说明理由.
PB,若存在,求出x的值;若不存在,说明理由.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形ABCD中,AB=2,BC=1,运点P从点B出发,沿路线B![]() C
C![]() D作匀速运动,那么△ABP的面积
D作匀速运动,那么△ABP的面积![]() 与点P运动的路程之间的函数图象大致是( ).
与点P运动的路程之间的函数图象大致是( ).

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了美化校园计划购买茶花、桂花两种树苗共600株,茶花树苗每株35元,桂花树苗每株40元.相关资料表明:茶花、桂花树苗的成活率分别为80%,90%.
(1)若购买这两种树苗共用去22000元,则茶花、桂花树苗各购买多少株?
(2)若要使这批树苗的总成活率不低于85%,则茶花树苗至多购买多少株?
(3)在(2)的条件下,应如何选购树苗,使购买树苗的费用最低,并求出最低费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分8分)
如图,点E,F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O.

(1)求证:AB=DC;
(2)试判断△OEF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=10,BC=16.点D在边BC上,且点D到边AB和边AC的距离相等.
(1)用直尺和圆规作出点D(不写作法,保留作图痕迹,在图上标注出点D);
(2)求点D到边AB的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是半圆直径,半径OC⊥AB于点O,D为半圆上一点,AC∥OD,AD与OC交于点E,连结CD、BD,给出以下三个结论:①OD平分∠COB;②BD=CD;③CD2=CECO,其中正确结论的序号是 . 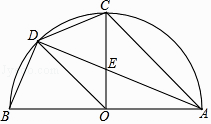
查看答案和解析>>
科目:初中数学 来源: 题型:
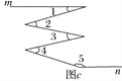
【题目】如图,在图a、图b、图c中都有直线m∥n,
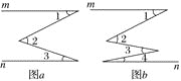
(1)在图a中,∠2和∠1、∠3之间的数量关系是__________________.
(2)猜想:在图b中,∠1、∠2、∠3、∠4之间的数量关系是____________________.
(3)猜想:在图c中,∠2、∠4和∠1、∠3、∠5的数量关系式是____________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com