
【题目】如图1,在平面直角坐标系中,直线![]() :
:![]() 与
与![]() 轴相交于B,与
轴相交于B,与![]() 轴相交于点A.直线
轴相交于点A.直线![]() :
:![]() 经过原点,并且与直线
经过原点,并且与直线![]() 相交于C点.
相交于C点.
(1)求ΔOBC的面积;
(2)如图2,在![]() 轴上有一动点E,连接CE.问CE+
轴上有一动点E,连接CE.问CE+![]() BE是否有最小值,如果有,求出相应的点E的坐标及CE+
BE是否有最小值,如果有,求出相应的点E的坐标及CE+![]() BE的最小值;如果没有,请说明理由;
BE的最小值;如果没有,请说明理由;
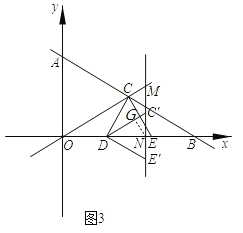
(3)如图3,在(2)的条件下,以CE为一边作等边ΔCDE,D点正好落在![]() 轴上.将ΔDCE绕点D顺时针旋转,旋转角度为
轴上.将ΔDCE绕点D顺时针旋转,旋转角度为![]() (0°≤
(0°≤![]() ≤360),记旋转后的三角形为ΔDCE′,点C,E的对称点分别为C′,E′.在旋转过程中,设C′E′所在的直线与直线
≤360),记旋转后的三角形为ΔDCE′,点C,E的对称点分别为C′,E′.在旋转过程中,设C′E′所在的直线与直线![]() 相交于点M,与
相交于点M,与![]() 轴正半轴相交于点N.当ΔOMN为等腰三角形时,求线段ON的长?
轴正半轴相交于点N.当ΔOMN为等腰三角形时,求线段ON的长?

【答案】(1) ![]() ;(2)E(6,0),最小值为
;(2)E(6,0),最小值为![]() .(3) ON=
.(3) ON=![]() 或3-
或3-![]() 或6或3
或6或3![]() 3或3
3或3![]() +3.
+3.
【解析】
(1)求出点B、C的坐标,就可以求出△OBC的面积;
(2)作点C关于x轴的对称点P,作射线BP,过点C作CH⊥BP交x轴于点E,则CE+![]() BE有最小值;
BE有最小值;
(3)分两种情况:∠MON为等腰三角形的顶角或底角.
(1)如图1,易求点B(9,0),解方程组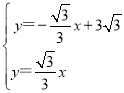 得:
得: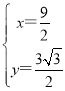 ;
;
故点C(![]() ,
,![]() ),
),
∴S△OBC=![]() ×9×
×9×![]() =
=![]() .
.
(2)如图2,作点C关于x轴的对称点P,作射线BP,过点E作EH⊥BP于点H,取BE中点I,连接HI.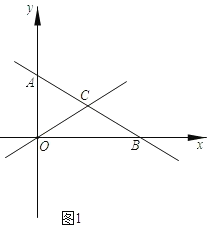
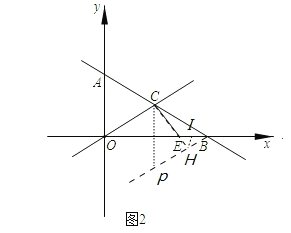
易知:∠BOC=∠OBC=∠OBP=30°,∠BHE=90°,
∵IE=IB,
∴IH=IE=IB
∵∠BEH=60°,
∴△EIH是等边三角形,
∴EH=EI=![]() EB,
EB,
∴当C、E、H三点共线且CH⊥BP时,CH的长度最小,即CE+![]() BE有最小值;
BE有最小值;
∵OC=CB=3![]() ,∠BCH=30°,∠BHC=90°,
,∠BCH=30°,∠BHC=90°,
∴BH=![]() BC=
BC=![]()
∴CH=![]()
=![]()
故CE+![]() BE有最小值为
BE有最小值为![]() .
.
在Rt△BEH中,∵∠EBH=30°,
∴EH=![]() BE,
BE,
∵BE2-EH2=BH2
∴BE=3
∴E(6,0).
(3)△OMN为等腰三角形,分三种情况:
①当∠OMN=∠ONM时,
∵∠MON=30°,

∴∠OMN=∠ONM=75°
如图3,当∠OMN=∠ONM=75°时,∠C′DN=45°,∠DC′N=60°,
∴∠CDC′=α=15°,过点N作NG⊥DC′于G,
可求得GC′=![]() ,
,
∴ON=![]()
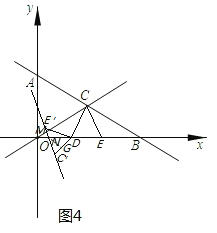
如图4,当∠OMN=∠ONM=75°时,∠C′DN=45°,旋转角α=195°
过点N作NG⊥DC′于G,
可求得DN=![]() ,
,
∴ON=3-![]() ,
,
②如图5,当∠OMN=∠MON=30°时,∠ONM=120°,
此时旋转角α=60°,易得ON=6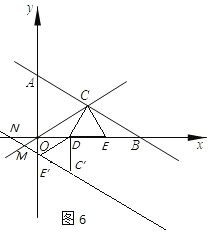

③如图6,图7,当∠ONM=∠NOM=30°时,
∴∠OMN=120°,
∵∠DE′C′=60°,α=150°或330°,
∴DE′∥OM,
过点E′作E′G⊥x轴于G,可求得DN=3![]() ,
,
∴ON=3![]() 3或3
3或3![]()
综上所述,ON=![]() 或3-
或3-![]() 或6或3
或6或3![]() 3或3
3或3![]() +3.
+3.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
【题目】平面直角坐标系中有正方形AOBC,O为坐标原点,点A、B分别在y轴、x轴正半轴上,点P、E、F分别为边BC、AC、OB上的点,EF⊥OP于M.
(1)如图1,若点E与点A重合,点A坐标为(0,8),OF=3,求P点坐标;
(2)如图2,若点E与点A重合,且P为边BC的中点,求证:CM=2CP;
(3)如图3,若点M为线段OP的中点,连接AB交EF于点N,连接NP,试探究线段OP与NP的数量关系,并证明你的结论.



查看答案和解析>>
科目:初中数学 来源: 题型:
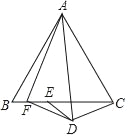
【题目】如图,△ABC是边长为24的等边三角形,△CDE是等腰三角形,其中DC=DE=10,∠CDE=120°,点E在BC边上,点F是BE的中点,连接AD、DF、AF,则AF的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:
对于线段的垂直平分线我们有如下结论:到线段两个端点距离相等的点在线段的垂直平分线上.即如图①,若PA=PB,则点P在线段AB的垂直平分线上.

请根据阅读材料,解决下列问题:
如图②,直线CD是等边△ABC的对称轴,点D在AB上,点E是线段CD上的一动点(点E不与点C、D重合),连结AE、BE,△ABE经顺时针旋转后与△BCF重合.
(1)旋转中心是点 ,旋转了 (度);
(2)当点E从点D向点C移动时,连结AF,设AF与CD交于点P,在图②中将图形补全,并探究∠APC的大小是否保持不变?若不变,请求出∠APC的度数;若改变,请说出变化情况.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从三角形(不是等腰三角形)一个顶点引出一条射线于对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.
(1)如图1,在△ABC中,CD为角平分线,∠A=40°,∠B=60°,求证:CD为△ABC的完美分割线.
(2)在△ABC中,∠A=48°,CD是△ABC的完美分割线,且△ACD为等腰三角形,求∠ACB的度数.
(3)如图2,△ABC中,AC=2,BC=![]() ,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长.
,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长.
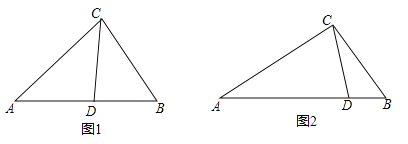
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用A、B两种机器人搬运大米,A型机器人比B型机器人每小时多搬运20袋大米,A型机器人搬运700袋大米与B型机器人搬运500袋大米所用时间相等.求A、B型机器人每小时分别搬运多少袋大米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2) 如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=![]() ,其中
,其中![]() 为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
(3)拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABD和△ACD关于直线AD对称;在射线AD上取点E,连接BE, CE,如图:在射线AD上取点F连接BF, CF,如图,依此规律,第n个图形中全等三角形的对数是( )

A.nB.2n-1C.![]() D.3(n+1)
D.3(n+1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com