
【题目】如图,已知矩形ABCD和BCEF,AF=BE,AF与BE交于点G,∠AGB=60°.
(1)求证:AF=DE;
(2)若AB=6,BC=8,求AF.
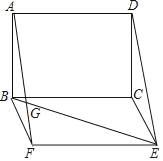
【答案】(1)证明见解析;(2)AF=10.
【解析】
(1)欲证明AF=DE,只要证明四边形ADEF是平行四边形即可;
(2)连接BD.利用勾股定理求出BD,再证明△BDE是等边三角形即可.
(1)∵四边形ABCD是矩形,
∴AD∥BC,AD=BC,
∵四边形BCEF是平行四边形,
∴BC∥EF,BC=EF,
∴AD=EF,AD∥EF,
∴四边形ADEF是平行四边形,
∴AF=DE;
(2)连接BD,
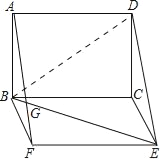
∵四边形ABCD是矩形,
∴∠BCD=90°,CD=AB=6,
∵BC=8,
∴BD=![]() =10,
=10,
∵四边形ADEF是平行四边形,
∴AF∥DE,
∴∠AGB=∠BED=60°,
∵AF=DE=BE,
∴△BDE是等边三角形,
∴AF=BE=BD=10.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】四张小卡片上分别写有数字1、2、3、4,它们除数字外没有任何区别,现将它们放在盒子里搅匀.
(1)随机地从盒子里抽取一张,求抽到数字3的概率;
(2)随机地从盒子里抽取一张,将数字记为x,不放回再抽取第二张,将数字记为y,请你用画树状图或列表的方法表示所有等可能的结果,并求出点(x,y)在函数![]() 图象上的概率.
图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
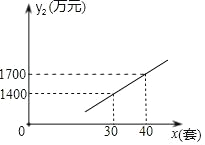
【题目】国家推行“节能减排,低碳经济”政策后,某环保节能设备生产企业的产品供不应求.若该企业的某种环保设备每月的产量保持在一定的范围,每套产品的生产成本不高于50万元,每套产品的售价不低于80万元,已知这种设备的月产量x(套)与每套的售价y(万元)之间满足关系式y=150﹣2x,月产量x(套)与生产总成本y2(万元)存在如图所示的函数关系.
(1)直接写出y2与x之间的函数关系式;
(2)求月产量x的范围;
(3)当月产量x(套)为多少时,这种设备的利润W(万元)最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年12月9日诸暨迎来首届马拉松盛典——西施马拉松。我们一起用“诸暨精神”见证了“诸暨奇迹”!马拉松期间为了缓解市区内一些主要路段交通拥挤的现状,市交警队在一些主要路口设立了交通路况显示牌(如图).已知立杆AB高度是3m,从侧面D点测得显示牌顶端C点和底端B点的仰角分别是60°和45°.求路况显示牌BC的高度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°, AD是∠BAC的平分线,O是AB上一点, 以OA为半径的⊙O经过点D.

(1)求证:BC是⊙O切线;
(2)若BD=5,DC=3,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从热气球C处测得地面A、B两点的俯角分别为45°、30°,如果此时热气球C处离地面的高度CD为100米,且点A、D、B在同一直线上,求AB两点间的距离(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课本中有一道作业题:有一块三角形余料ABC,它的边BC=120mm,高AD=80mm.要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.
(1)加工成的正方形零件的边长是多少mm?
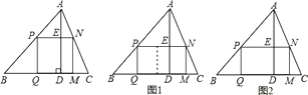
(2)如果原题中要加工的零件是一个矩形,且此矩形是由两个并排放置的正方形所组成,如图1,此时,这个矩形零件的两条边长又分别为多少?请你计算.
(3)如果原题中所要加工的零件只是一个矩形,如图2,这样,此矩形零件的两条边长就不能确定,但这个矩形面积有最大值,求达到这个最大值时矩形零件的两条边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,若将△ABC绕点C顺时针旋转180°得到△EFC,连接AF、BE.
(1)求证:四边形ABEF是平行四边形;
(2)当∠ABC为多少度时,四边形ABEF为矩形?请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com