
【题目】如图,在△ABC中,∠C=90°, AD是∠BAC的平分线,O是AB上一点, 以OA为半径的⊙O经过点D.

(1)求证:BC是⊙O切线;
(2)若BD=5,DC=3,求AC的长.
【答案】(1)证明见解析;(2)6.
【解析】试题分析:(1)要证BC是⊙O的切线,只要连接OD,再证OD⊥BC即可.
(2)过点D作DE⊥AB,根据角平分线的性质可知CD=DE=3,由勾股定理得到BE的长,再通过证明△BDE∽△BAC,根据相似三角形的性质得出AC的长.
试题解析:(1)证明:连接OD;
∵AD是∠BAC的平分线,
∴∠1=∠3.
∵OA=OD,
∴∠1=∠2.
∴∠2=∠3.
∴OD∥AC.
∴∠ODB=∠ACB=90°.
∴OD⊥BC.
∴BC是⊙O切线.
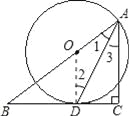
(2)解:过点D作DE⊥AB,
∵AD是∠BAC的平分线,
∴CD=DE=3.
在Rt△BDE中,∠BED=90°,
由勾股定理得: ![]() ,
,
∵∠BED=∠ACB=90°,∠B=∠B,
∴△BDE∽△BAC.
∴![]() .
.
∴![]() .
.
∴AC=6.


 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:初中数学 来源: 题型:
【题目】下列尺规作图的语句正确的是( )
A. 延长射线AB到D B. 以点D为圆心,任意长为半径画弧
C. 作直线AB=3cm D. 延长线段AB至C,使AC=BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个正比例函数与一个一次函数的图象交于点A(3,4),其中一次函数与y轴交于B点,且OA=OB.

(1)求这两个函数的表达式;
(2)求△AOB的面积S.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ABC,△ADE为等腰直角三角形,∠ACB=∠AED=90°.(1)如图1,点E在AB上,点D与C重合,F为线段BD的中点.则线段EF与FC的数量关系是 ;∠EFD的度数为 ;
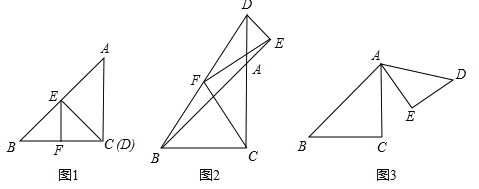
(2)如图2,在图1的基础上,将△ADE绕A点顺时针旋转到如图2的位置,其中D、A、C在一条直线上,F为线段BD的中点.则线段EF与FC是否存在某种确定的数量关系和位置关系?证明你的结论;
(3)若△ADE绕A点任意旋转一个角度到如图③的位置,F为线段BD的中点,连接EF、FC,请你完成图3,请猜想线段EF与FC的关系,并验证你的猜想.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com