
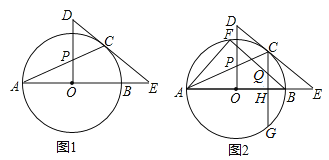
【题目】如图1,AB是⊙O的直径,E是AB延长线上一点,EC切⊙O于点C,OP⊥AO交AC于点P,交EC的延长线于点D.
(1)求证:△PCD是等腰三角形;
(2)CG⊥AB于H点,交⊙O于G点,过B点作BF∥EC,交⊙O于点F,交CG于Q点,连接AF,如图2,若sinE=![]() ,CQ=5,求AF的值.
,CQ=5,求AF的值.
【答案】(1)证明见解析;(2)12.
【解析】
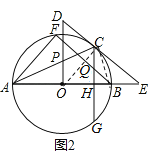
试题分析:(1)连接OC,由切线性质和垂直性质得∠1+∠3=90°、∠2+∠4=90°,继而可得∠3=∠5得证;
(2)连接OC、BC,先根据切线性质和平行线性质及垂直性质证∠BCG=∠QBC得QC=QB=5,而sinE=sin∠ABF=![]() ,可知QH=3、BH=4,设圆的半径为r,在RT在△OCH中根据勾股定理可得r的值,在RT△ABF中根据三角函数可得答案.
,可知QH=3、BH=4,设圆的半径为r,在RT在△OCH中根据勾股定理可得r的值,在RT△ABF中根据三角函数可得答案.
试题解析:(1)连接OC,∵EC切⊙O于点C,∴OC⊥DE,∴∠1+∠3=90°,又∵OP⊥OA,∴∠2+∠4=90°,∵OA=OC,∴∠1=∠2,∴∠3=∠4,又∵∠4=∠5,∴∠3=∠5,∴DP=DC,即△PCD为等腰三角形;
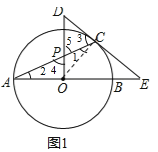
(2)如图2,连接OC、BC.∵DE与⊙O相切于点E,∴∠OCB+∠BCE=90°,∵OC=OB,∴∠OCB=∠OBC,∴∠OBC+∠BCE=90°,又∵CG⊥AB,∴∠OBC+∠BCG=90°,∴∠BCE=∠BCG,∵BF∥DE,∴∠BCE=∠QBC,∴∠BCG=∠QBC,∴QC=QB=5,∵BF∥DE,∴∠ABF=∠E,∵sinE=![]() ,∴sin∠ABF=
,∴sin∠ABF=![]() ,∴QH=3、BH=4,设⊙O的半径为r,∴在△OCH中,
,∴QH=3、BH=4,设⊙O的半径为r,∴在△OCH中,![]() ,解得:r=10,又∵∠AFB=90°,sin∠ABF=
,解得:r=10,又∵∠AFB=90°,sin∠ABF=![]() ,∴AF=12.
,∴AF=12.


科目:初中数学 来源: 题型:
【题目】甲、乙两人在5次打靶测试中命中的环数如下: 甲:8,8,7,8,9
乙:5,9,7,10,9
(1)填写下表:
平均数 | 众数 | 中位数 | 方差 | |
甲 | 8 | 8 | 0.4 | |
乙 | 9 | 3.2 |
(2)教练根据这5次成绩,选择甲参加射击比赛,教练的理由是什么?
(3)如果乙再射击1次,命中8环,那么乙的射击成绩的方差 . (填“变大”、“变小”或“不变”).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线MN是四边形AMBN的对称轴,点P是直线MN上的点,下列判断错误的是( )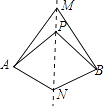
A.AM=BM
B.AP=BN
C.∠MAP=∠MBP
D.∠ANM=∠BNM
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,点D在AB上,将△BCD绕点C按顺时针方向旋转90°后得△ECF.
(1)补充完成图形;
(2)若EF∥CD,求证:∠BDC=90°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某书店为了迎接“读书节”制定了活动计划,以下是活动计划书的部分信息:
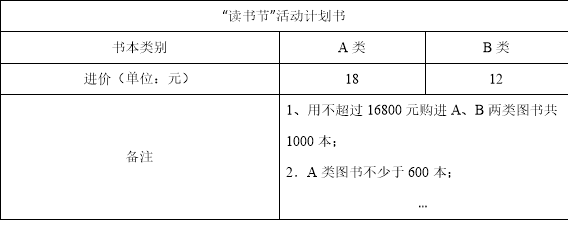
(1)陈经理查看计划数时发现:A类图书的标价是B类图书标价的1.5倍,若顾客用540元购买的图书,能单独购买A类图书的数量恰好比单独购买B类图书的数量少10本,请求出A、B两类图书的标价;
(2)经市场调查后,陈经理发现他们高估了“读书节”对图书销售的影响,便调整了销售方案,A类图书每本标价降低a元(0<a<5)销售,B类图书价格不变,那么书店应如何进货才能获得最大利润?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年国家将扩大公共场所免费上网范围,某小区响应号召调查小区居民上网费用情况,随机抽查了30户家庭的月上网费用,结果如表
月网费(元) | 50 | 100 | 150 |
户数(人) | 15 | 12 | 3 |
则关于这30户家庭的月上网费用,中位数是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】200粒大米重约4克,如果每人每天浪费1粒米,那么约458万人口的漳州市每天浪费大米用科学记数法表示约为( )
A.9.16×103克B.9.16×104克C.9,16×105克D.0.916×105克
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com