Question

8．已知二次函数y=-x²+2x+3
（1）作出该二次函数的图象，并写出对称轴和顶点坐标；
（2）结合该二次函数的图象，确定当x取何值时，y=0，y＞0，y＜0；
（3）当x取何值时，y的值随x值的增大而增大？当x取何值时，y随x的增大而减小？

Answer 1

分析 （1）将抛物线的一般式化为顶点式，就可以确定对称轴，顶点，要求抛物线与x轴的交点，就要把解析式化为交点式，即可得到与坐标轴交点的坐标；
（2）根据图象与x轴的交点坐标，可确定y=0，y＞0，y＜0时，x的取值范围；
（3）根据对称轴左右两侧图象的上升和下降趋势确定函数的增减性．

解答 解：（1））∵y=-x²+2x+3，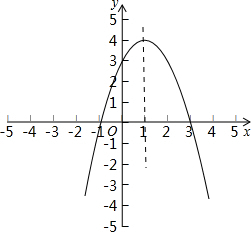
=-（x-1）²+4，
=-（x-3）（x+1）
∴顶点（1，4），对称轴x=1，与x轴交点（3，0），（-1，0），与y轴交点（0，3）；
如右图所示：
（2）由图象可知：
当y=0时，x=-1或x=3；
当y＞0时，-1＜x＜3；
当y＜0时，x＜-1或x＞3；
（3）∵对称轴x=1，抛物线开口向下，
∴当x＜1时，y的值随x值的增大而增大；
当x＞1时，y随x的增大而减小．

点评 本题主要考查了抛物线的对称轴、顶点坐标与抛物线解析式的关系以及利用图象确定自变量的取值范围和增减性，抛物线的顶点式：y=a（x-h）²+k，顶点坐标为（h，k），对称轴x=h．用抛物线与x轴的交点坐标，判断函数值的符号以及函数的增减性要注意数形结合．