
(如图,已知∠AOB=ll0°,∠AOC=m∠AOD,∠COE=n∠BOC,且3(m-2)+4=m+2,单项式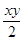 的系数为n.
的系数为n.
(1)求4(m-n) 2-(m-n) 2-5的值;
(2)当∠COD:∠COE=3:2时,试求∠COD的度数.
(1) ;(2)33°
;(2)33°
解析试题分析:(1)先解方程3(m-2)+4=m+2得到m的值,再根据单项式的系数的定义得到n的值,然后化简代数式,最后代入求值;
(2)由(1)可知∠AOC =2∠AOD,∠COE= ∠BOC,则可得∠AOD=
∠BOC,则可得∠AOD= ∠AOC,∠COD=∠AOC-∠AOD=
∠AOC,∠COD=∠AOC-∠AOD= ∠AOC,从而求得∠COD+∠COE=55°,设∠COD=3x°,则∠COE=2x°,即可列方程求解.
∠AOC,从而求得∠COD+∠COE=55°,设∠COD=3x°,则∠COE=2x°,即可列方程求解.
(1)解方程3(m-2)+4=m+2得m="2"
由已知有n=
∴4(m-n)2-(m-n)2-5=3(m-n)2-5
当m=2,n= 时,m-n=
时,m-n= ,原式=3×(
,原式=3×( )2-5=
)2-5= -5=
-5= ;
;
(2)由(1)可知:∠AOC =2∠AOD,∠COE= ∠BOC
∠BOC
∴∠AOD= ∠AOC,∠COD=∠AOC-∠AOD=
∠AOC,∠COD=∠AOC-∠AOD= ∠AOC
∠AOC
∴∠COD+∠COE= (∠AOC+∠BOC)=
(∠AOC+∠BOC)= ∠AOB=55°
∠AOB=55°
设∠COD=3x°,则∠COE=2x°
∴3x+2x=55
∴x=11
∴∠COD=33°.
考点:代数式求值,一元一次方程的应用
点评:本题知识点较多,综合性强,难度较大,需要学生熟练掌握各方面的基础知识.


科目:初中数学 来源: 题型:


查看答案和解析>>
科目:初中数学 来源: 题型:
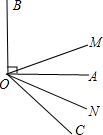
| A、45° | ||
B、45°+
| ||
C、60°-
| ||
| D、不能计算 |
查看答案和解析>>
科目:初中数学 来源: 题型:
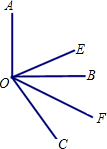 如图,已知∠AOB是直角,∠BOC=60°,OE平分∠AOC,OF平分∠BOC.
如图,已知∠AOB是直角,∠BOC=60°,OE平分∠AOC,OF平分∠BOC.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知∠AOB=x(0°<x<180°),OC平分∠AOB,点N为OB上一个定点.通过画图可以知道:当∠AOB=45°时,在射线OC上存在点P,使△ONP成为等腰三角形,且符合条件的点有三个,即P1(顶点为P2),P2(顶点为0),P3(顶点为N).
如图,已知∠AOB=x(0°<x<180°),OC平分∠AOB,点N为OB上一个定点.通过画图可以知道:当∠AOB=45°时,在射线OC上存在点P,使△ONP成为等腰三角形,且符合条件的点有三个,即P1(顶点为P2),P2(顶点为0),P3(顶点为N).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com