解:(1)∵E、F分别是AB、BC的中点,AB=120米,BC=200米,
∴AE=BE=60米,BF=CF=100米;
当公交公司在E点设一公交停靠站点,则从三个小区大门步行到公交停靠点的路程长之和为:
AE+BE+CE,
=AB+BC+BE,
=120+200+60,
=380(米);
当公交公司在F点设一公交停靠站点,则从三个小区大门步行到公交停靠点的路程长之和为:
AF+BF+CF,
=AB+BF+BC,
=120+100+200,
=420(米);
∵380<420,
∴公交车停靠点的位置应该是点E处;
(2)①根据题意,得
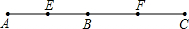
,
∵E、F分别是AB、BC的中点,
∴EB=

AB,BF=

BC;
又∵EF=EB+BF,
∴EF=

(AB+BC)=

(a+b);
②

此时FB=

b,EB=

a,
EF=FB-EB=

(b-a).
分析:(1)根据图示,先分别计算一下从三个小区大门步行到公交停靠点E、F的路程长之和,然后比较一下大小,路程小的即为所求;
(2)根据题意,画出图示,根据图示找出EF与AB、BC的数量关系,注意分类讨论.
点评:本题主要考查了两点间的距离.解答本题是,采用了数形结合的数学思想,降低了题目的难度.


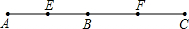 ,
, AB,BF=
AB,BF= BC;
BC; (AB+BC)=
(AB+BC)= (a+b);
(a+b);
 b,EB=
b,EB= a,
a, (b-a).
(b-a).

 如图,已知A,B两点是反比例函数y=
如图,已知A,B两点是反比例函数y=