练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    请你写出一个b的值，使得函数y=x2+2bx，在x＞0时，y的值随着x的值增大而增大，则b可以是
     
    ．
    考点：二次函数的性质
    专题：开放型
    分析：由二次函数开口向上，可知在对称轴右侧y随x的增大而增大，可先求出其对称轴，只要满足对称轴小于或等于0即可．
    解答：解：∵函数y=x2+2bx，
    ∴其对称轴为x=-b，开口向上，
    ∴当-b≤0时，在x＞0时，y的值随x的增大而增大，
    ∴可取b为1，
    故答案为：1．
    点评：本题主要考查抛物线的对称轴和增减性，掌握开口向上的二次函数在对称轴右侧y随x的增大而增大是解题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

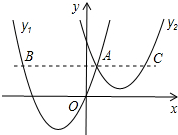    如图，抛物线y1=a（x+2）2-3与y2=
    1
    2
    （x-3）2+1交于点A（1，3），过点A作x轴的平行线，分别交两条抛物线于点B，C 则以下结论：①无论x取何值，y2的值总是正数；②a=1；③y1与y2共有三个交点；④2AB=3AC；其中正确结论有（　　）个．
    A、1个B、2个C、3个D、4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，AD∥BE∥FC，它们依次交直线l1、l2于点A、B、C和点D、E、F．如果AB=2，BC=3，那么
    DE
    EF
    的值是
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，AD平分∠BAC，BD⊥AD，DE∥AC，求证：△BDE是等腰三角形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，已知抛物线y=
    1
    7
    x2+bx+c    与x轴的正半轴交于A，B两点，AB=4，P为抛物线上的一点，它的横坐标为-1，∠PAB=135°，过P作PM⊥x轴于点M，BM：PM=7：3．
    （1）求点P的坐标；
    （2）求抛物线的解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

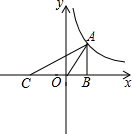    如图，直线AC：y=x+k与双曲线y=
    k
    x
    的图象在第一象限相交于A，C是直线y=x+k与x轴的交点，过A作AB垂直x轴于点B，且S△AOB=3．
    （1）求k的值；
    （2）求S△ABC的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    阅读，如果x1，x2是一元二次方程ax2+bx+c=0的两根，那么有x1+x2=-
    b
    a
    ，x1x2=
    c
    a
    ．这是一元二次方程根与系数的关系，我们可以用它来解题．应用：已知x1，x2是方程2x2-6x-1=0的两根，则（x1-x2）2的值为
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

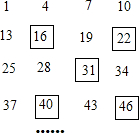    将一定规律的一组数1，4，7，10，13…排成如下表，并象如图一样对称框住其中五个数（阴影部分），请你仔细观察框住的五个数字规律，并回答下列问题：
    （1）对称框住五个数的和与中间的数码31有什么关系？
    （2）设对称框住五个数的中间的数为x，用代数式表示这五个数的和；
    （3）若象如图一样上下左右移动对称框，框住另外的五个数，这五个数的和能等于2015吗？如能，写出这五个数；如不能，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    下列函数中是反比例函数的有
     
      （填序号）．
    ①y=-
    x
    3
    ； ②y=-
    2
    x
    ； ③y=
    -3
    2x
    ； ④xy=
    1
    2
    ； ⑤y=x-1； ⑥
    y
    x
    =2    ； ⑦y=
    k
    x
    （k为常数，k≠0）

    查看答案和解析>>

    同步练习册答案