
 如图,已知第一象限内的点A在反比例函数y=
如图,已知第一象限内的点A在反比例函数y=| 2 |
| x |
| k |
| x |
| ||
| 3 |
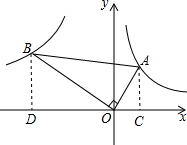 解:作AC⊥x轴于点C,作BD⊥x轴于点D.
解:作AC⊥x轴于点C,作BD⊥x轴于点D.
| ||
| 3 |
| 2 |
| S△OBD |
| S△AOC |
| OB |
| OA |
| 1 |
| 2 |


科目:初中数学 来源: 题型:
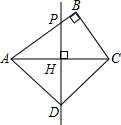 如图,已知PH是Rt△ABC斜边AC上的垂直平分线,垂足为点H,并交直角边AB于点P,D是PH上一点,且AD是AP与AB的比例中项.求证:
如图,已知PH是Rt△ABC斜边AC上的垂直平分线,垂足为点H,并交直角边AB于点P,D是PH上一点,且AD是AP与AB的比例中项.求证:查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
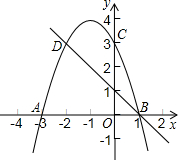 如图,二次函数的图象与x轴相交于A(-3,0)、B(1,0)两点,与y轴相交于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.
如图,二次函数的图象与x轴相交于A(-3,0)、B(1,0)两点,与y轴相交于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.查看答案和解析>>
科目:初中数学 来源: 题型:
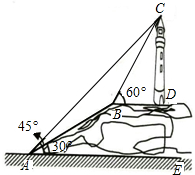 如图,某教学学习小组为了测量山顶上一古灯塔的高度CD,他们在山脚下的点A处测得塔顶C处的仰角为45°,沿着坡角为30°的登山梯AB向上走200米到达山顶B处后,测得塔顶C处的仰角为60°,已知点B与底部D在同一水平线上.
如图,某教学学习小组为了测量山顶上一古灯塔的高度CD,他们在山脚下的点A处测得塔顶C处的仰角为45°,沿着坡角为30°的登山梯AB向上走200米到达山顶B处后,测得塔顶C处的仰角为60°,已知点B与底部D在同一水平线上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com