
【题目】如图,直线m的解析表达式为:y=-3x+3,且m与![]() 轴交于点D,直线n经过点A、B,直线m,n交于点C.
轴交于点D,直线n经过点A、B,直线m,n交于点C.
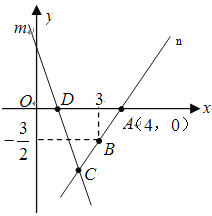
(1)求点D的坐标;
(2)求直线n的解析表达式;
(3)求△ADC的面积;
(4)在直线n上存在异于点C的另一点P,使得△ADP与△ADC的面积相等,写出点P的坐标
【答案】(1)D(1,0)(2)y=![]() x-6(3)
x-6(3)![]() (4)(6,3)
(4)(6,3)
【解析】
试题分析:(1)y=-3x+3,令y=0,求出点D的横坐标即可;(2)设直线l2的解析表达式为y=kx+b,把点AB的坐标代入得出方程组,然后解方程组即可;(3)求出两条直线的交点C的坐标,然后利用三角形的面积公式计算即可;(4)当AP=AC时,△ADP与△ADC的面积相等,根据AC的长即可求出点P的坐标.
试题解析:(1)由y=-3x+3,令y=0,得-3x+3=0,∴x=1,∴D(1,0);
(2)设直线l2的解析表达式为y=kx+b,由图象知:x=4,y=0;x=3,![]() ,∴4k+b=0,
,∴4k+b=0,![]() ,
,
∴b=-6,![]() ,∴直线l2的解析表达式为
,∴直线l2的解析表达式为![]() ;
;
(3)由y=-3x+3,![]() ,解得x=2,y=-3,∴C(2,-3),∵AD=3,∴
,解得x=2,y=-3,∴C(2,-3),∵AD=3,∴![]() ;
;
(4)P(6,3).


 寒假学与练系列答案
寒假学与练系列答案科目:初中数学 来源: 题型:
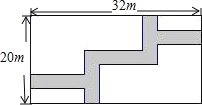
【题目】如图,在宽为20m,长为32m的矩形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上草坪.要使草坪的面积为540m2,求道路的宽.
(部分参考数据:322=1024,522=2704,482=2304)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在边BC上以每秒1个单位长的速度由点C向点B运动.

(1)当t为何值时,四边形PODB是平行四边形?
(2)在线段PB上是否存在一点Q,使得ODQP为菱形?若存在,求t的值;若不存在,请说明理由;
(3)△OPD为等腰三角形时,写出点P的坐标(不必写过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为促进江南新区的发展,長江三桥在区政府的统一指导下夜以继日的修建中,为方便残疾人通行,政府计划在位于南滨路桥头处修建一锲形残疾人通道,如图,该楔形斜坡BC长20米,坡角为12°,区领导为进一步方便残疾人的轮椅车通行,准备把坡角降为5°.

(1)求斜坡新起点到原起点B的距离(精确到0.1米)
(参考数据:sin12°≈0.21,cos12°≈0.98,tan5°≈0.09)
(2)某6人工程队承担这项改进任务(假设每人毎天的工怍效率相同),5天刚好完成该项工程;但实际工作
2天后.有2人因其它工作调离;剩余的工程由余下的4人独自完成,为了不延误工期,每人的工作效率提高了a%,结果准时完成该项工程,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知三角形的两边长是2 cm,3 cm,则该三角形的周长l的取值范围是( )
A. 1<l<5 B. 1<l<6
C. 5<l<9 D. 6<l<10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】你能求(x﹣1)(x99+x98+x97+…+x+1)的值吗?
遇到这样的问题,我们可以先思考一下,从简单的情形入手.先计算下列各式的值:
(1)(x﹣1)(x+1)= ;
(2)(x﹣1)(x2+x+1)= ;
(3)(x﹣1)(x3+x2+x+1)= ;
由此我们可以得到(x﹣1)(x99+x98+…+x+1)= ;
请你利用上面的结论,完成下面两题的计算:
(1)299+298+…+2+1;
(2)(﹣3)50+(﹣3)49+…+(﹣3)+1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)|﹣2|﹣(2﹣π)0+![]() +(﹣2)3
+(﹣2)3
(2)(﹣2x3)2(﹣x2)÷[(﹣x)2]3
(3)(x+y)2(x﹣y)2
(4)(x﹣2y+3z)(x+2y﹣3z)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com