分析:(1)两圆内切,通常是作两圆的公切线,此题也不例外.过P作两圆的公切线MN,根据弦切角定理,易证得∠MPA=∠PCB=∠D,而AD是⊙O2切线,所以∠PCD=∠PBC,由此可证得△PBC∽△PCD,即可得到∠1=∠2.
(2)通过(1)题相似三角形所得到的比例线段,即可得到PC2=PB•PD,根据韦达定理可知PB•PD=4,由此可求出PC的长.
(3)由于△PBC和△APC等高不同底,所以面积比等于底边的比,即AB:AP=(k-1):k;由于弧BP=弧BC,则∠1=∠BCP=∠2,由此可证得PD∥BC,则△ABC∽△APD,故BC:PD=(k-1):k,而BC=PB,代入上式可求得PD的表达式,根据韦达定理可求得PB+PD的值,即可得到PB的表达式,将PB、PD的值代入PB•PD=4中,即可求出代数式的值.
解答: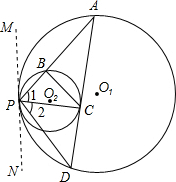
(1)证明:过P作两圆的公切线MN,则有:
∠MPA=∠PCB=∠D;
又∵AD是⊙O
2的切线,
∴∠PCD=∠PBC,
∴△PBC∽△PCD,
∴∠1=∠2.
(2)解:由(1)知:△PBC∽△PCD,得:
PB:PC=PC:PD,即PC
2=PB•PD;
∵PB、PD的长是关于x的方程
x2-x+4=0的两个根,
∴PB•PD=4,
∴PC
2=4,即PC=2.
(3)解:∵S
△PBC:S
△APC=1:k,
∴AP:BP=k:1,即AB:AP=(k-1):1;
∵
=,
∴∠1=∠BCP,BP=BC;
又∵∠1=∠2,
∴∠2=∠BCP;
∴BC∥PD,
∴△ABC∽△APD,
∴
=,即
=;
∴
=,即PB=
PD,
又∵PB+PD=
,
∴PB=
,PD=
;
∵PB•PD=4,即:
×
=4,
化简得:k(k-1)(m+16)=4(2k-1)2,即:
(m+16)k
2-(m+16)k=16k
2-16k+4,
mk
2-mk=4,即m(k
2-k)=4.
点评:此题主要考查了韦达定理,弦切角定理,圆心角、弧、弦的关系以及相似三角形的判定和性质等知识,第(3)问的计算量较大,难点在于不知如何下手,能够通过相似三角形和韦达定理得到PB、PD的表达式是解决此题的关键.

 O1于D,且PB、PD的长恰好是关于x的方程x2-
O1于D,且PB、PD的长恰好是关于x的方程x2- (1)证明:过P作两圆的公切线MN,则有:
(1)证明:过P作两圆的公切线MN,则有:



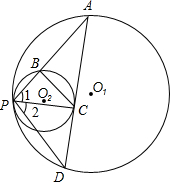
 12、已知:如图,⊙O1与⊙O2外切于点P,直线AB过点P交⊙O1于A,交⊙O2于B,点C、D分别为⊙O1、⊙O2上的点,且∠ACP=65°,则∠BDP=
12、已知:如图,⊙O1与⊙O2外切于点P,直线AB过点P交⊙O1于A,交⊙O2于B,点C、D分别为⊙O1、⊙O2上的点,且∠ACP=65°,则∠BDP=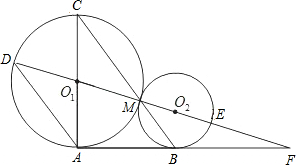 已知:如图,⊙O1与⊙O2外切于M点,AF是两圆的外公切线,A、B是切点,DF经过O1、O2,分别交⊙O1于D、⊙O2于E,AC是⊙O1的直径,BC经过M点,连接AD.
已知:如图,⊙O1与⊙O2外切于M点,AF是两圆的外公切线,A、B是切点,DF经过O1、O2,分别交⊙O1于D、⊙O2于E,AC是⊙O1的直径,BC经过M点,连接AD.