
【题目】如图,已知点A从点(1,0)出发,以1个单位长度/秒的速度沿x轴向正方向运动,以O、A为顶点作菱形OABC,使点B、C在第一象限内,且∠AOC=60°,点P的坐标为(0,3),设点A运动了t秒,求:
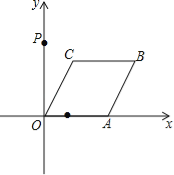
(1)点C的坐标(用含t的代数式表示);
(2)点A在运动过程中,当t为何值时,使得△OCP为等腰三角形?
【答案】(1)点C的坐标为:(![]() (1+t),
(1+t),![]() (1+t));(2)当t=
(1+t));(2)当t=![]() ﹣1,t=2,t=3
﹣1,t=2,t=3![]() ﹣1时,均可使得△OCP为等腰三角形.
﹣1时,均可使得△OCP为等腰三角形.
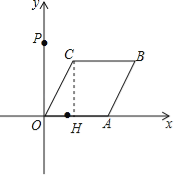
【解析】试题分析:(1)过点C作CH⊥x轴于点H,解直角三角形CHO,求出OH,CH的长,即可求出点C的坐标;
(2)因为等腰三角形OCP的腰和底不确定所以要分三种情况分别讨论:①当以O为等腰三角形顶点时;②当以C为等腰三角形顶点时;③当以P为等腰三角形顶点时,求出t的值即可.
解:(1)过点C作CH⊥x轴于点H,
根据题意得:OA=1+t,
∵四边形OABC是菱形,
∴OC=OA=1+t,
∵∠AOC=60°,
∴OH="OC"![]() cos60°=
cos60°=![]() OC=
OC=![]() (1+t),CH="OC"
(1+t),CH="OC"![]() sin60°=
sin60°=![]() (1+t),
(1+t),
∴点C的坐标为:(![]() (1+t),
(1+t),![]() (1+t));
(1+t));
(2)①当以O为等腰三角形顶点时,OC=OP,
∴1+t=3,
∴t=2;
②当以C为等腰三角形顶点时,PC=OC,则CH=![]() OP=
OP=![]() ,
,
即![]() (1+t)=
(1+t)=![]() ,
,
解得:t=![]() ﹣1;
﹣1;
③当以P为等腰三角形顶点时,OP=PC,∠POC=30°,则Q(0,![]() ),
),
∴OC=3![]() ,
,
∴1+t=3![]() ,
,
∴t=3![]() ﹣1,
﹣1,
综上可知,当t=![]() ﹣1,t=2,t=3
﹣1,t=2,t=3![]() ﹣1时,均可使得△OCP为等腰三角形.
﹣1时,均可使得△OCP为等腰三角形.


科目:初中数学 来源: 题型:
【题目】小李对初三(1)班全体同学的业余兴趣爱好(第一爱好)进行了一次调查,她根据采集到的数据,绘制了下面的图1和图2.

请你根据图中提供的信息,解答下列问题:
(1)初三(1)班共有学生________人;
(2)在图1中,将“书画”部分的图形补充完整;
(3)在图2中,“球类”部分所对应的圆心角的度数________度;爱好“音乐”的人数占本班学生数的百分数是________;爱好“书画”的人数占本班学生数的百分数是________;“其它”的人数占本班学生数的百分数是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司需招聘一名员工,对应聘者甲、乙、丙从笔试、面试、体能三个方面进行量化考核.甲、乙、丙各项得分如下表:
笔 试 | 面 试 | 体 能 | |
甲 | 85 | 80 | 75 |
乙 | 80 | 90 | 73 |
丙 | 83 | 79 | 90 |
(1)根据三项得分的平均分,从高到低确定三名应聘者的排名顺序.
(2)该公司规定:笔试,面试、体能得分分别不得低于80分,80分,70分,并按60%,30%,10%的比例计入总分(不计其他因素条件),请你说明谁将被录用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,∠A=60°,点D是BC边的中点,作射线DE,与边AB交于点E,射线DE绕点D顺时针旋转120°,与直线AC交于点F.
(1)依题意将图1补全;
(2)小华通过观察、实验提出猜想:在点E运动的过程中,始终有DE=DF.小华把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法:
想法1:由点D是BC边的中点,通过构造一边的平行线,利用全等三角形,可证DE=DF;
想法2:利用等边三角形的对称性,作点E关于线段AD的对称点P,由∠BAC与∠EDF互补,可得∠AED与∠AFD互补,由等角对等边,可证DE=DF;
想法3:由等腰三角形三线合一,可得AD是∠BAC的角平分线,由角平分线定理,构造点D到AB,AC的高,利用全等三角形,可证DE=DF….
请你参考上面的想法,帮助小华证明DE=DF(选一种方法即可);
(3)在点E运动的过程中,直接写出BE,CF,AB之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是矩形,把矩形沿AC折叠,点B落在点E处,AE与DC的交点为O,连接DE.
(1)求证:△ADE≌△CED;
(2)求证:DE∥AC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校计划购买一批篮球和足球,已知购买2个篮球和1个足球共需320元,购买3个篮球和2个足球共需540元.
(1)求每个篮球和每个足球的售价;
(2)如果学校计划购买这两种球共50个,总费用不超过5500元,那么最多可购买多少个足球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们用[a]表示不大于a的最大整数,例如:[2.5]=2,[3]=3,[-2.5]=-3;用<a>表示大于a的最小整数,例如:<2.5>=3,<3>=4,<-2.5>=-2.根据上述规定,解决下列问题:
(1)[-4.5]=______,<3.01>=____;
(2)若x为整数,且[x]+<x>=2 017,求x的值;
(3)若x,y满足方程组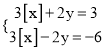 ,求x,y的取值范围.
,求x,y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了更好地保护环境,某区污水处理厂决定购买A,B两种型号污水处理设备10台,其中每台的价格、月处理污水量如下表.已知购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元.

(1)求a,b的值;
(2)某区污水处理厂决定购买污水处理设备的资金既不少于108万元也不超过110万元,问有几种购买方案?每月最多能处理污水多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形OABC的边长为2,顶点A,C分别在x轴的负半轴和y轴的正半轴上,M是BC的中点,P(0,m)是线段OC上一动点(C点除外),直线PM交AB的延长线于点D.
(1)求点D的坐标(用含m的代数式表示);
(2)当△APD是以AP为腰的等腰三角形时,求m的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com