
【题目】我们用[a]表示不大于a的最大整数,例如:[2.5]=2,[3]=3,[-2.5]=-3;用<a>表示大于a的最小整数,例如:<2.5>=3,<3>=4,<-2.5>=-2.根据上述规定,解决下列问题:
(1)[-4.5]=______,<3.01>=____;
(2)若x为整数,且[x]+<x>=2 017,求x的值;
(3)若x,y满足方程组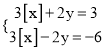 ,求x,y的取值范围.
,求x,y的取值范围.
【答案】(1) -5, 4;(2)x=1 008;(3)-1≤x<0,2≤y<3.
【解析】试题分析: (1)根据[a]表示不大于a的最大整数,<a>表示大于a的最小整数,进行计算即可;
(2)根据[x]+<x>=2017,可得x+(x+1)=2017,进而得到x=1008;
(3)解方程组可得![]() ,再根据[a]表示不大于a的最大整数,<a>表示大于a的最小整数,即可得到x、y的取值范围.
,再根据[a]表示不大于a的最大整数,<a>表示大于a的最小整数,即可得到x、y的取值范围.
试题解析:
:(1)由题可得[-4.5]=-5,<3.01>=4,
故答案为:-5,4;
(2)∵[x]≤x,且x为整数,
∴[x]=x,
∵<x>>x,且x为整数,
∴<x>=x+1,
∵[x]+<x>=2017,
∴x+(x+1)=2017,
解得x=1008;
(3)解原方程组,得![]()
又∵[x]表示不大于x的最大整数,<x>表示大于x的最小整数,
∴-1≤x<0,2≤y<3.


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2的图象与一次函数y=x+b的图象相交于A(﹣2,2)、B两点,从点A和点B分别引平行于y轴的直线与x轴分别交于C,D两点,点P(t,0),为线段CD上的动点,过点P且平行于y轴的直线与抛物线和直线分别交于R,S.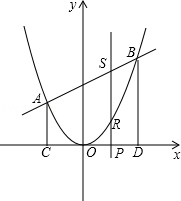
(1)求一次函数和二次函数的解析式,并求出点B的坐标;
(2)当SR=2RP时,计算线段SR的长;
(3)若线段BD上有一动点Q且其纵坐标为t+3,问是否存在t的值,使S△BRQ=15?若存在,求t的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填空或填写理由.
(1)如图甲,∵∠ =∠ (已知);
∴AB∥CD( )
(2)如图乙,已知直线a∥b,∠3=80°,求∠1,∠2的度数.
解:∵a∥b,( )
∴∠1=∠4( )
又∵∠3=∠4( )
∠3=80°(已知)
∴∠1=( )(等量代换)
又∵∠2+∠3=180°
∴∠2=( )(等式的性质)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A从点(1,0)出发,以1个单位长度/秒的速度沿x轴向正方向运动,以O、A为顶点作菱形OABC,使点B、C在第一象限内,且∠AOC=60°,点P的坐标为(0,3),设点A运动了t秒,求:
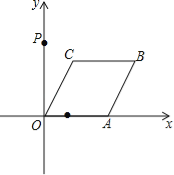
(1)点C的坐标(用含t的代数式表示);
(2)点A在运动过程中,当t为何值时,使得△OCP为等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对![]() ,
, ![]() 定义一种新运算
定义一种新运算![]() ,规定
,规定![]() (其中
(其中![]() ,
, ![]() 均为非零常数),这里等式右边是通常的四则运算,例:
均为非零常数),这里等式右边是通常的四则运算,例: ![]() .
.
已知![]() ,
, ![]() .
.
(1)求![]() ,
, ![]() 的值;
的值;
(2)若关于m的不等式组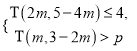 恰好有3个整数解,求实数
恰好有3个整数解,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在数学课上,老师提出如下问题:
作图:过直线外一点作已知直线的平行线.
已知:直线l及其外一点A.
求作:l的平行线,使它经过点A.

小天利用直尺和三角板进行如下操作:如图所示:
①用三角板的斜边与已知直线l重合;
②用直尺紧靠三角板一条直角边;
③沿着直尺平移三角板,使三角板的斜边通过已知点A;
④沿着这条斜边画一条直线,所画直线与已知直线平行.
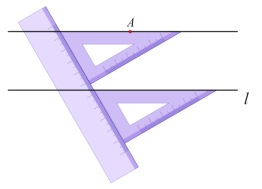
老师说:“小天的作法正确.”
请回答:小天的作图依据是___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y=kx﹣4k+5的图象与反比例函数y= ![]() (x>0)的图象相交于点A(p,q).当一次函数y的值随x的值增大而增大时,p的取值范围是 .
(x>0)的图象相交于点A(p,q).当一次函数y的值随x的值增大而增大时,p的取值范围是 . 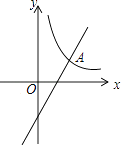
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中错误的是( )
A. 若∠C=∠A–∠B,则△ABC为直角三角形
B. 若a∶b∶c=2∶2∶2![]() ,则△ABC为直角三角形
,则△ABC为直角三角形
C. 若a=![]() c,b=
c,b=![]() c,则△ABC为直角三角形
c,则△ABC为直角三角形
D. 若∠A∶∠B∶∠C=3∶4∶5,则△ABC为直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(南阳唐河县期中)如图,在ABCD中,DE平分∠ADC交AB于G,交CB的延长线于E,BF平分∠ABC交AD的延长线于F.
(1)若AD=5,AB=8,求GB的长;
(2)求证:∠E=∠F.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com