
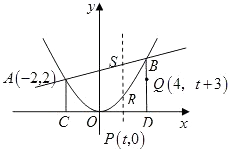
【题目】如图,二次函数y=ax2的图象与一次函数y=x+b的图象相交于A(﹣2,2)、B两点,从点A和点B分别引平行于y轴的直线与x轴分别交于C,D两点,点P(t,0),为线段CD上的动点,过点P且平行于y轴的直线与抛物线和直线分别交于R,S.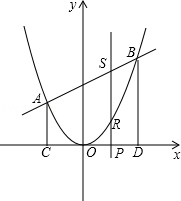
(1)求一次函数和二次函数的解析式,并求出点B的坐标;
(2)当SR=2RP时,计算线段SR的长;
(3)若线段BD上有一动点Q且其纵坐标为t+3,问是否存在t的值,使S△BRQ=15?若存在,求t的值;若不存在,说明理由.
【答案】
(1)
解:由题意知点A(﹣2,2)在y=ax2的图象上,又在y=x+b的图象上
所以得2=a(﹣2)2和2=﹣2+b,
∴ ![]() ,b=4.
,b=4.
∴一次函数的解析式为y=x+4.
二次函数的解析式为y= ![]() x2.
x2.
由  ,
,
解得 ![]() 或
或 ![]() ,
,
所以B点的坐标为(4,8)
(2)
解:因过点P(t,0)且平行于y轴的直线为x=t,
![]() 得
得 ![]() ,
,
所以点S的坐标(t,t+4).
由 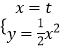 得
得 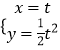 ,
,
所以点R的坐标(t, ![]() t2).
t2).
所以SR=t+4﹣ ![]() t2,RP=
t2,RP= ![]() t2.
t2.
由SR=2RP得t+4﹣ ![]() t2=2×
t2=2× ![]() t2,
t2,
解得 ![]() 或t=2.
或t=2.
因点P(t,0)为线段CD上的动点,
所以﹣2≤t≤4,
所以 ![]() 或t=2
或t=2
当t=2时,SR=2+4﹣ ![]() ×22=4
×22=4
所以线段SR的长为 ![]() 或4
或4
(3)
解:存在符合题意的t.
因BQ=8﹣(t+3)=5﹣t,点R到直线BD的距离为4﹣t,
所以S△BRQ= ![]() (5﹣t)(4﹣t)=15.
(5﹣t)(4﹣t)=15.
解得t=﹣1或t=10.
因为﹣2≤t≤4,
所以t=﹣1.
【解析】(1)将A点坐标分别代入抛物线和直线的解析式中即可求出两函数的解析式.然后联立两函数的函数式即可求出B点的坐标.(2)线段SR实际是直线AB的函数值和抛物线函数值的差.而RP的长实际是R点的纵坐标,根据SR=2RP可得出一个关于P点横坐标t的方程,据此可求出P点的横坐标t.然后代入SR的表达式即可求出SR的长.(3)可用t表示出BQ的长,再根据D,P的坐标用t表示出R到BD的距离,然后根据三角形的面积公式即可得出△BRQ的面积表达式,根据其面积为15可求出t的值.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:
【题目】已知n边形的内角和θ=(n-2)×180°.
(1)甲同学说,θ能取360°;而乙同学说,θ也能取630°.甲、乙的说法对吗?若对,求出边数n.若不对,说明理由;
(2)若n边形变为(n+x)边形,发现内角和增加了360°,用列方程的方法确定x.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AE∥BF,AC平分∠BAE,交BF于C. 
(1)尺规作图:过点B作AC的垂线,交AC于O,交AE于D,(保留作图痕迹,不写作法);
(2)求证:AD=BC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小李对初三(1)班全体同学的业余兴趣爱好(第一爱好)进行了一次调查,她根据采集到的数据,绘制了下面的图1和图2.

请你根据图中提供的信息,解答下列问题:
(1)初三(1)班共有学生________人;
(2)在图1中,将“书画”部分的图形补充完整;
(3)在图2中,“球类”部分所对应的圆心角的度数________度;爱好“音乐”的人数占本班学生数的百分数是________;爱好“书画”的人数占本班学生数的百分数是________;“其它”的人数占本班学生数的百分数是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学习了统计知识后,班主任王老师叫班长就本班同学的上学方式进行了一次调查统计,图1和图2是他通过收集数据后,绘制的两幅不完整的统计图,请你根据图中提供的信息,解答以下问题: 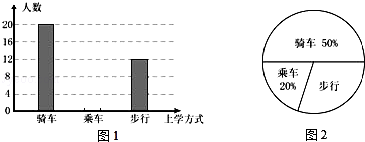
(1)在扇形统计图中,计算出“步行”部分所对应的圆心角的度数;
(2)求该班共有多少名学生;
(3)在图1中,将表示“乘车”的部分补充完整.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现
如图1,点E.F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF、则EF=BE+DF,试说明理由;
(2)类比引申
如图2,在四边形ABCD中,AB=AD,∠BAD=90°,点E.F分别在边BC、CD上,∠EAF=45°,若∠B,∠D都不是直角,则当∠B与∠D满足等量关系 时,仍有EF=BE+DF;
(3)联想拓展
如图3,在△ABC中,∠BAC=90°,AB=AC,点D、E均在边BC上,且∠DAE=45°,猜想BD、DE、EC满足的等量关系,并写出推理过程。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在四边形ABCD中,AD∥BC,AB=AD,∠BAD的平分线AE交BC于点E,连接DE.
(1)求证:四边形ABED是菱形;
(2)若∠DEC=60°,CE=2DE=4cm,求CD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司需招聘一名员工,对应聘者甲、乙、丙从笔试、面试、体能三个方面进行量化考核.甲、乙、丙各项得分如下表:
笔 试 | 面 试 | 体 能 | |
甲 | 85 | 80 | 75 |
乙 | 80 | 90 | 73 |
丙 | 83 | 79 | 90 |
(1)根据三项得分的平均分,从高到低确定三名应聘者的排名顺序.
(2)该公司规定:笔试,面试、体能得分分别不得低于80分,80分,70分,并按60%,30%,10%的比例计入总分(不计其他因素条件),请你说明谁将被录用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们用[a]表示不大于a的最大整数,例如:[2.5]=2,[3]=3,[-2.5]=-3;用<a>表示大于a的最小整数,例如:<2.5>=3,<3>=4,<-2.5>=-2.根据上述规定,解决下列问题:
(1)[-4.5]=______,<3.01>=____;
(2)若x为整数,且[x]+<x>=2 017,求x的值;
(3)若x,y满足方程组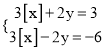 ,求x,y的取值范围.
,求x,y的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com