
【题目】(1)问题发现
如图1,点E.F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF、则EF=BE+DF,试说明理由;
(2)类比引申
如图2,在四边形ABCD中,AB=AD,∠BAD=90°,点E.F分别在边BC、CD上,∠EAF=45°,若∠B,∠D都不是直角,则当∠B与∠D满足等量关系 时,仍有EF=BE+DF;
(3)联想拓展
如图3,在△ABC中,∠BAC=90°,AB=AC,点D、E均在边BC上,且∠DAE=45°,猜想BD、DE、EC满足的等量关系,并写出推理过程。

【答案】(1)详见解析;(2)详见解析;(3)详见解析.
【解析】试题分析:(1)把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合,证出△AFG≌△AFE,根据全等三角形的性质得出EF=FG,即可得出答案;
(2)把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合,证出△AFE≌△AFG,根据全等三角形的性质得出EF=FG,即可得出答案;
(3)把△ACE旋转到ABF的位置,连接DF,证明△AFE≌△AFG(SAS),则EF=FG,∠C=∠ABF=45°,△BDF是直角三角形,根据勾股定理即可作出判断.
试题解析:(1)理由是:如图1,
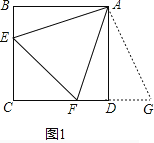
∵AB=AD,
∴把△ABE绕点A逆时针旋转90至△ADG,可使AB与AD重合,如图1,
∵∠ADC=∠B=90,
∴∠FDG=180,点F. D. G共线,
则∠DAG=∠BAE,AE=AG,
∠FAG=∠FAD+∠GAD=∠FAD+∠BAE=9045=45=∠EAF,
即∠EAF=∠FAG,
在△EAF和△GAF中,
AF=AF,∠EAF=∠GAF,AE=AG,
∴△AFG≌△AFE(SAS),
∴EF=FG=BE+DF;
(2)∠B+∠D=180时,EF=BE+DF;
∵AB=AD,
∴把△ABE绕点A逆时针旋转90至△ADG,可使AB与AD重合,如图2,
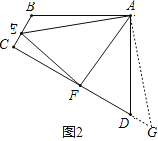
∴∠BAE=∠DAG,
∵∠BAD=90,∠EAF=45,
∴∠BAE+∠DAF=45,
∴∠EAF=∠FAG,
∵∠ADC+∠B=180,
∴∠FDG=180,点F. D. G共线,
在△AFE和△AFG中,
AE=AG,∠FAE=∠FAG,AF=AF,
∴△AFE≌△AFG(SAS),
∴EF=FG,
即:EF=BE+DF,
故答案为:∠B+∠ADC=180;
(3)BD2+CE2=DE2.
理由是:把△ACE旋转到ABF的位置,连接DF,
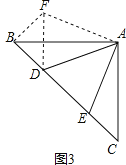
则∠FAB=∠CAE.
∵∠BAC=90,∠DAE=45,
∴∠BAD+∠CAE=45,
又∵∠FAB=∠CAE,
∴∠FAD=∠DAE=45,
则在△ADF和△ADE中,
AD=AD,∠FAD=∠DAE,AF=AE,
∴△ADF≌△ADE,
∴DF=DE,∠C=∠ABF=45,
∴∠BDF=90,
∴△BDF是直角三角形,
∴BD2+BF2=DF2,
∴BD2+CE2=DE2.


科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,直线PQ垂直平分AC,与边AB交于E,连接CE,过点C作CF平行于BA交PQ于点F,连接AF.
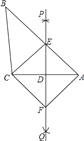
(1)求证:△AED≌△CFD;
(2)求证:四边形AECF是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一种公益叫“光盘”.所谓“光盘”,就是吃光你盘子中的食物,杜绝“舌尖上的浪费”.某校九年级开展“光盘行动”宣传活动,根据各班级参加该活动的总人次折线统计图,下列说法正确的是( )

A. 极差是40 B. 中位数是58 C. 平均数大于58 D. 众数是5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2的图象与一次函数y=x+b的图象相交于A(﹣2,2)、B两点,从点A和点B分别引平行于y轴的直线与x轴分别交于C,D两点,点P(t,0),为线段CD上的动点,过点P且平行于y轴的直线与抛物线和直线分别交于R,S.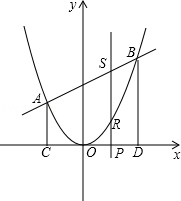
(1)求一次函数和二次函数的解析式,并求出点B的坐标;
(2)当SR=2RP时,计算线段SR的长;
(3)若线段BD上有一动点Q且其纵坐标为t+3,问是否存在t的值,使S△BRQ=15?若存在,求t的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在我国古代数学著作《九章算术》中记载了一道有趣的数学问题:“今有凫(凫:野鸭)起南海,七日至北海;雁起北海,九日至南海.今凫雁俱起,问何日相逢?”意思是:野鸭从南海起飞,7天飞到北海;大雁从北海起飞,9天飞到南海.野鸭与大雁从南海和北海同时起飞,经过几天相遇.设野鸭与大雁从南海和北海同时起飞,经过x天相遇,根据题意,下面所列方程正确的是( )
A.(9﹣7)x=1
B.(9+7)x=1
C.( ![]() +
+ ![]() )x=1
)x=1
D.( ![]() ﹣
﹣ ![]() )x=1
)x=1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,AD=6.M、N分别是AB、CD边的中点,P是AD上的点,且∠PNB=3∠CBN.
(1)求证:∠PNM=2∠CBN;
(2)求线段AP的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD绕点A按逆时针方向旋转,得到矩形AEFG,E点正好落在边CD上,连接BE,BG,且BG交AE于P.
(1)求证:∠CBE=![]() ∠BAE;
∠BAE;
(2)求证:PG=PB;
(3)若AB=![]() ,BC=3,求出BG的长.
,BC=3,求出BG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在数学课上,老师提出如下问题:
作图:过直线外一点作已知直线的平行线.
已知:直线l及其外一点A.
求作:l的平行线,使它经过点A.

小天利用直尺和三角板进行如下操作:如图所示:
①用三角板的斜边与已知直线l重合;
②用直尺紧靠三角板一条直角边;
③沿着直尺平移三角板,使三角板的斜边通过已知点A;
④沿着这条斜边画一条直线,所画直线与已知直线平行.
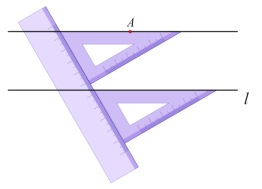
老师说:“小天的作法正确.”
请回答:小天的作图依据是___________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com