
����Ŀ���Ķ�������ϣ�
����ѧ���ϣ���ʦ����������⣺
��ͼ����ֱ����һ������ֱ֪�ߵ�ƽ���ߣ�
��֪��ֱ��l������һ��A��
������l��ƽ���ߣ�ʹ��������A��

С������ֱ�ߺ����ǰ�������²�������ͼ��ʾ��
�������ǰ��б������ֱ֪��l�غϣ�
����ֱ�߽������ǰ�һ��ֱ�DZߣ�
������ֱ��ƽ�����ǰ���ʹ���ǰ��б��ͨ����֪��A��
����������б��һ��ֱ��������ֱ������ֱ֪��ƽ��.
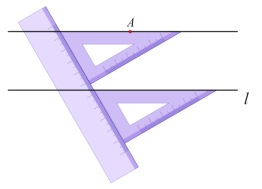
��ʦ˵����С���������ȷ����
��ش�С�����ͼ������___________��
 ÿ�α���ϵ�д�
ÿ�α���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(1)���ⷢ��
��ͼ1,��E.F�ֱ���������ABCD�ı�BC��CD��,��EAF=45�㣬����EF����EF=BE+DF����˵�����ɣ�
(2)�������
��ͼ2,���ı���ABCD��,AB=AD,��BAD=90��,��E.F�ֱ��ڱ�BC��CD��,��EAF=45�㣬����B����D������ֱ�ǣ���B���D���������ϵ ʱ������EF=BE+DF��
(3)������չ
��ͼ3,�ڡ�ABC��,��BAC=90��,AB=AC,��D��E���ڱ�BC��,�ҡ�DAE=45�㣬����BD��DE��EC����ĵ�����ϵ����д���������̡�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У�AB=AC����A=60�㣬��D��BC�ߵ��е㣬������DE�����AB���ڵ�E������DE�Ƶ�D˳ʱ����ת120�㣬��ֱ��AC���ڵ�F��
��1�������⽫ͼ1��ȫ��
��2��С��ͨ���۲졢ʵ��������룺�ڵ�E�˶��Ĺ����У�ʼ����DE=DF��С�������������ͬѧ�ǽ��н�����ͨ�����ۣ��γ���֤���ò���ļ����뷨��
�뷨1���ɵ�D��BC�ߵ��е㣬ͨ������һ�ߵ�ƽ���ߣ�����ȫ�������Σ���֤DE=DF��
�뷨2�����õȱ������εĶԳ��ԣ�����E�����߶�AD�ĶԳƵ�P���ɡ�BAC���EDF�������ɵá�AED���AFD�������ɵȽǶԵȱߣ���֤DE=DF��
�뷨3���ɵ������������ߺ�һ���ɵ�AD�ǡ�BAC�Ľ�ƽ���ߣ��ɽ�ƽ���߶����������D��AB��AC�ĸߣ�����ȫ�������Σ���֤DE=DF����
����ο�������뷨������С��֤��DE=DF��ѡһ�ַ������ɣ���
��3���ڵ�E�˶��Ĺ����У�ֱ��д��BE��CF��AB֮���������ϵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ�ƻ�����һ�������������֪����2�������1��������320Ԫ������3�������2��������540Ԫ��
��1����ÿ�������ÿ��������ۼۣ�
��2�����ѧУ�ƻ�������������50�����ܷ��ò�����5500Ԫ����ô���ɹ�����ٸ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������[a]��ʾ������a��������������磺[2.5]��2��[3]��3��[��2.5]����3���ã�a����ʾ����a����С���������磺��2.5����3����3����4������2.5������2.���������涨������������⣺
(1)[��4.5]��______����3.01����____��
(2)��xΪ��������[x]����x����2 017����x��ֵ��
(3)��x��y���㷽����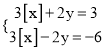 ����x��y��ȡֵ��Χ��
����x��y��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AD��BC���ϵĸߣ�AE����BAC��ƽ���ߣ���B=40�㣬��DAE=15�㣬����C�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˸��õر���������ij����ˮ��������������A��B�����ͺ���ˮ�����豸10̨������ÿ̨�ļ۸��´�����ˮ�����±�����֪����һ̨A���豸�ȹ���һ̨B���豸��2��Ԫ������2̨A���豸�ȹ���3̨B���豸��6��Ԫ��

��1����a��b��ֵ��
��2��ij����ˮ����������������ˮ�����豸���ʽ�Ȳ�����108��ԪҲ������110��Ԫ�����м��ֹ���?ÿ������ܴ�����ˮ���ٶ�?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��PA��PB�ֱ��С�O��A��B���㣬��C���Ż� ![]() �ϣ���P=80�㣬���C�Ķ���Ϊ�� ��
�ϣ���P=80�㣬���C�Ķ���Ϊ�� �� 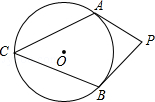
A.50��
B.60��
C.70��
D.80��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺��ij��������������A��B����ԭ��Գƣ���Ƹ�������Ϊ�����������ߡ�����֪���κ���y=ax2��2mx+c��a��m��c��Ϊ������ac��0���ǡ����������ߡ���
��1�����ж�ac�ķ��ţ�
��2����c=��1���ö��κ���ͼ����y�ύ�ڵ�C����S��ABC=1��
����a��ֵ��
�ڵ��ö��κ���ͼ����˵�ΪM����1��1����N��3��4�����߶�����ֻ��һ������ʱ����m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com