
【题目】有一种公益叫“光盘”.所谓“光盘”,就是吃光你盘子中的食物,杜绝“舌尖上的浪费”.某校九年级开展“光盘行动”宣传活动,根据各班级参加该活动的总人次折线统计图,下列说法正确的是( )

A. 极差是40 B. 中位数是58 C. 平均数大于58 D. 众数是5
 提分百分百检测卷系列答案
提分百分百检测卷系列答案科目:初中数学 来源: 题型:
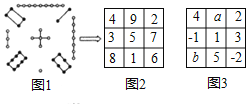
【题目】(阅读材料)“九宫图”源于我国古代夏禹时期的“洛书”![]() 图1所示
图1所示![]() ,是世界上最早的矩阵,又称“幻方”,用今天的数学符号翻译出来,“洛书”就是一个三阶“幻方”
,是世界上最早的矩阵,又称“幻方”,用今天的数学符号翻译出来,“洛书”就是一个三阶“幻方”![]() 图2所示
图2所示![]() .
.
(规律总结)观察图1、图2,根据“九宫图”中各数字之间的关系,我们可以总结出“幻方”需要满足的条件是______;若图3,是一个“幻方”,则![]() ______.
______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,制作某金属工具先将材料煅烧6分钟温度升到800℃,再停止煅烧进行锻造,8分钟温度降为600℃;煅烧时温度y(℃)与时间x(min)成一次函数关系;锻造时温度y(℃)与时间x(min)成反比例函数关系;该材料初始温度是32℃. 
(1)分别求出材料煅烧和锻造时y与x的函数关系式;
(2)根据工艺要求,当材料温度低于480℃时,须停止操作,那么锻造的操作时间有多长?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反映的是某中学九(3)班学生外出方式(乘车、步行、骑车)的频数(人数)分布直方图(部分)和扇形分布图,那么下列说法正确的是( )
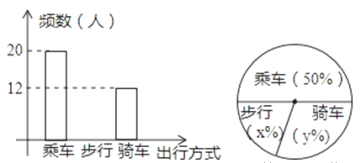
A. 九(3)班外出的学生共有42人
B. 九(3)班外出步行的学生有8人
C. 在扇形图中,步行的学生人数所占的圆心角为82°
D. 如果该校九年级外出的学生共有500人,那么估计全年级外出骑车的学生约有140人
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AE∥BF,AC平分∠BAE,交BF于C. 
(1)尺规作图:过点B作AC的垂线,交AC于O,交AE于D,(保留作图痕迹,不写作法);
(2)求证:AD=BC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AD=2AB,点E,F分别是AD,BC的中点,连接AF与BE,CE与DF分别交于点M,N两点,则四边形EMFN是( )
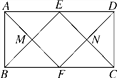
A. 正方形 B. 菱形 C. 矩形 D. 无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小李对初三(1)班全体同学的业余兴趣爱好(第一爱好)进行了一次调查,她根据采集到的数据,绘制了下面的图1和图2.

请你根据图中提供的信息,解答下列问题:
(1)初三(1)班共有学生________人;
(2)在图1中,将“书画”部分的图形补充完整;
(3)在图2中,“球类”部分所对应的圆心角的度数________度;爱好“音乐”的人数占本班学生数的百分数是________;爱好“书画”的人数占本班学生数的百分数是________;“其它”的人数占本班学生数的百分数是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现
如图1,点E.F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF、则EF=BE+DF,试说明理由;
(2)类比引申
如图2,在四边形ABCD中,AB=AD,∠BAD=90°,点E.F分别在边BC、CD上,∠EAF=45°,若∠B,∠D都不是直角,则当∠B与∠D满足等量关系 时,仍有EF=BE+DF;
(3)联想拓展
如图3,在△ABC中,∠BAC=90°,AB=AC,点D、E均在边BC上,且∠DAE=45°,猜想BD、DE、EC满足的等量关系,并写出推理过程。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,∠A=60°,点D是BC边的中点,作射线DE,与边AB交于点E,射线DE绕点D顺时针旋转120°,与直线AC交于点F.
(1)依题意将图1补全;
(2)小华通过观察、实验提出猜想:在点E运动的过程中,始终有DE=DF.小华把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法:
想法1:由点D是BC边的中点,通过构造一边的平行线,利用全等三角形,可证DE=DF;
想法2:利用等边三角形的对称性,作点E关于线段AD的对称点P,由∠BAC与∠EDF互补,可得∠AED与∠AFD互补,由等角对等边,可证DE=DF;
想法3:由等腰三角形三线合一,可得AD是∠BAC的角平分线,由角平分线定理,构造点D到AB,AC的高,利用全等三角形,可证DE=DF….
请你参考上面的想法,帮助小华证明DE=DF(选一种方法即可);
(3)在点E运动的过程中,直接写出BE,CF,AB之间的数量关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com