
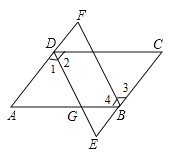
【题目】(南阳唐河县期中)如图,在ABCD中,DE平分∠ADC交AB于G,交CB的延长线于E,BF平分∠ABC交AD的延长线于F.
(1)若AD=5,AB=8,求GB的长;
(2)求证:∠E=∠F.

【答案】(1)3;(2)见解析
【解析】试题分析:(1)直接利用平行四边形的性质结合角平分线的性质得出∠2=∠AGD,进而得出AD=AG,得出答案即可;
(2)根据平行四边形的性质可得AF∥CE,根据平行四边形的性质和角平分线定义证明∠2=∠4,然后再证明ED∥FB,根据两组对边分别平行的四边形是平行四边形可得四边形BFDE是平行四边形,进而得出答案.
试题解析:(1)解:∵在ABCD中,DE平分∠ADC交AB于点G,BF平分∠ABC交AD的延长线于F,∴∠1=∠2,∠3=∠4,AB∥DC,∴∠2=∠AGD,∴∠1=∠AGD,∴AD=AG=5.∵AB=8,∴BG=8﹣5=3;
(2)证明:∵四边形ABCD是平行四边形,∴∠ADC=∠ABC,DC∥AB,AD∥BC.∵DE平分∠ADC,∴∠2=![]() ∠ADC.∵BF平分∠ABC,∴∠4=
∠ADC.∵BF平分∠ABC,∴∠4=![]() ∠ABC,∴∠2=∠4.∵DC∥AB,∴∠AGD=∠2,∴∠AGD=∠4,∴ED∥FB.∵AF∥CE,∴四边形BFDE是平行四边形,∴∠E=∠F.
∠ABC,∴∠2=∠4.∵DC∥AB,∴∠AGD=∠2,∴∠AGD=∠4,∴ED∥FB.∵AF∥CE,∴四边形BFDE是平行四边形,∴∠E=∠F.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:初中数学 来源: 题型:
【题目】我们用[a]表示不大于a的最大整数,例如:[2.5]=2,[3]=3,[-2.5]=-3;用<a>表示大于a的最小整数,例如:<2.5>=3,<3>=4,<-2.5>=-2.根据上述规定,解决下列问题:
(1)[-4.5]=______,<3.01>=____;
(2)若x为整数,且[x]+<x>=2 017,求x的值;
(3)若x,y满足方程组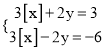 ,求x,y的取值范围.
,求x,y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果三角形满足一个角是另一个角的3倍,那么我们称这个三角形为“智慧三角形”.下列各组数据中,能作为一个智慧三角形三边长的一组是( )
A.1,2,3
B.1,1, ![]()
C.1,1, ![]()
D.1,2, ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形OABC的边长为2,顶点A,C分别在x轴的负半轴和y轴的正半轴上,M是BC的中点,P(0,m)是线段OC上一动点(C点除外),直线PM交AB的延长线于点D.
(1)求点D的坐标(用含m的代数式表示);
(2)当△APD是以AP为腰的等腰三角形时,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x、y的方程组![]() ,其中﹣3≤a≤1,给出下列说法:①当a=1时,方程组的解也是方程x+y=2﹣a的解;②当a=﹣2时,x、y的值互为相反数;③若x≤1,则1≤y≤4;④
,其中﹣3≤a≤1,给出下列说法:①当a=1时,方程组的解也是方程x+y=2﹣a的解;②当a=﹣2时,x、y的值互为相反数;③若x≤1,则1≤y≤4;④![]() 是方程组的解.其中说法错误的是( )
是方程组的解.其中说法错误的是( )
A. ①②③④ B. ①②③ C. ②④ D. ②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若某抛物线上有两点A、B关于原点对称,则称该抛物线为“完美抛物线”.已知二次函数y=ax2﹣2mx+c(a,m,c均为常数且ac≠0)是“完美抛物线”:
(1)试判断ac的符号;
(2)若c=﹣1,该二次函数图象与y轴交于点C,且S△ABC=1.
①求a的值;
②当该二次函数图象与端点为M(﹣1,1)、N(3,4)的线段有且只有一个交点时,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
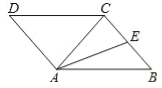
【题目】如图,在ABCD中,AC为对角线,AC=BC=5,AB=6,AE是△ABC的中线.
(1)用无刻度的直尺画出△ABC的高CH(保留画图痕迹);
(2)求△ACE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E. 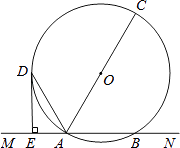
(1)求证:DE是⊙O的切线;
(2)若DE=6cm,AE=3cm,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个由5张纸片拼成的平行四边形,相邻纸片之间互不重叠也无缝隙,其中两张等腰直角三角形纸片的面积都为S1 , 另两张直角三角形纸片的面积都为S2 , 中间一张正方形纸片的面积为S3 , 则这个平行四边形的面积一定可以表示为( )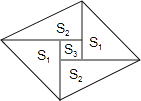
A.4S1
B.4S2
C.4S2+S3
D.3S1+4S3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com