
【题目】如图,直线AB、CD、BC分别与⊙O相切于E、F、G,且AB∥CD,若OB=6cm,OC=8cm,则BE+CG的长等于( )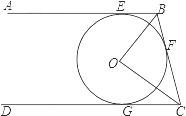
A.13
B.12
C.11
D.10
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,CD是一高为4米的平台,AB是与CD底部相平的一棵树,在平台顶C点测得树顶A点的仰角α=30°,从平台底部向树的方向水平前进3米到达点E,在点E处测得树顶A点的仰角β=60°,求树高AB(结果保留根号)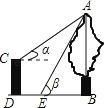
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:A(0,3),B(3,0),C(3,4)三点,点P(x,﹣0.5x),当△ABP的面积等于△ABC的面积时,则P点的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
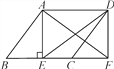
【题目】如图,在ABCD中,AE⊥BC于点E,延长BC至点F使CF=BE,连结AF,DE,DF.
(1)求证:四边形AEFD是矩形;
(2)若AB=6,DE=8,BF=10,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列方程变形正确的是( )
A.方程3x﹣2=2x﹣1移项,得3x﹣2x=﹣1﹣2
B.方程3﹣x=2﹣5(x﹣1)去括号,得3﹣x=2﹣5x﹣1
C.方程 ![]() 可化为3x=6.
可化为3x=6.
D.方程 ![]() 系数化为1,得x=﹣1
系数化为1,得x=﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC与BD交于点O.过点C作BD的平行线,过点D作AC的平行线,两直线相交于点E.
(1)求证:四边形OCED是矩形;
(2)若CE=1,DE=2,ABCD的面积是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线AB经过点A(6,0)、B(0,6),⊙O的半径为2(O为坐标原点),点P是直线AB上的一动点,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为( )
A.![]()
B.3
C.3 ![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某高楼顶部有一信号发射塔,在矩形建筑物ABCD的A、C两点测得该塔顶端F的仰角分别为45°和60°,矩形建筑物宽度AD=20m,高度DC=30m则信号发射塔顶端到地面的高度(即FG的长)为( )
A.(35 ![]() +55)m
+55)m
B.(25 ![]() +45)m
+45)m
C.(25 ![]() +75)m
+75)m
D.(50+20 ![]() )m
)m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图 1,在 ABCD 中,AC、BD 交于点 O,过点 O 的直线 l 交 AB 于 E, 交 CD 于 F,①判断 OE 和 OF 的数量关系: ,并证明;
② S四边形AEFD S四边形CFEB (填“>” 或“=” 或“<”).
(2)如图 2 是一块“L”形的材料,请你作一条直线 m,使得直线 m 两边的材料的面积相等(保留作图痕迹,不用证明).
(3)如图 3,正方形 ABCD 的边长为 2![]() cm,动点 P、Q 分别从点 A、C 同时出发,以 相同的速度分别沿 AD、CB 向终点 D、B 移动,当点 P 到达点 D 时,运动停止,过点 C 作 CH⊥PQ,垂足为点 H,连接 BH,则 BH 长的最小值为 cm(保留作图痕迹, 直接填写结果).
cm,动点 P、Q 分别从点 A、C 同时出发,以 相同的速度分别沿 AD、CB 向终点 D、B 移动,当点 P 到达点 D 时,运动停止,过点 C 作 CH⊥PQ,垂足为点 H,连接 BH,则 BH 长的最小值为 cm(保留作图痕迹, 直接填写结果).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com