
ЁОЬтФПЁПЃЈ1ЃЉШчЭМ 1ЃЌдк ABCD жаЃЌACЁЂBD НЛгкЕу OЃЌЙ§Еу O ЕФжБЯп l НЛ AB гк EЃЌ НЛ CD гк FЃЌЂйХаЖЯ OE КЭ OF ЕФЪ§СПЙиЯЕЃК ЃЌВЂжЄУїЃЛ
Ђк SЫФБпаЮAEFD SЫФБпаЮCFEB ЃЈЬюЁА>ЁБ ЛђЁА=ЁБ ЛђЁА<ЁБЃЉЃЎ
ЃЈ2ЃЉШчЭМ 2 ЪЧвЛПщЁАLЁБаЮЕФВФСЯЃЌЧыФузївЛЬѕжБЯп mЃЌЪЙЕУжБЯп m СНБпЕФВФСЯЕФУцЛ§ЯрЕШЃЈБЃСєзїЭМКлМЃЃЌВЛгУжЄУїЃЉЃЎ
ЃЈ3ЃЉШчЭМ 3ЃЌе§ЗНаЮ ABCD ЕФБпГЄЮЊ 2![]() cmЃЌЖЏЕу PЁЂQ ЗжБ№ДгЕу AЁЂC ЭЌЪБГіЗЂЃЌвд ЯрЭЌЕФЫйЖШЗжБ№би ADЁЂCB ЯђжеЕу DЁЂB вЦЖЏЃЌЕБЕу P ЕНДяЕу D ЪБЃЌдЫЖЏЭЃжЙЃЌЙ§Еу C зї CHЁЭPQЃЌДЙзуЮЊЕу HЃЌСЌНг BHЃЌдђ BH ГЄЕФзюаЁжЕЮЊ cmЃЈБЃСєзїЭМКлМЃЃЌ жБНгЬюаДНсЙћЃЉЃЎ
cmЃЌЖЏЕу PЁЂQ ЗжБ№ДгЕу AЁЂC ЭЌЪБГіЗЂЃЌвд ЯрЭЌЕФЫйЖШЗжБ№би ADЁЂCB ЯђжеЕу DЁЂB вЦЖЏЃЌЕБЕу P ЕНДяЕу D ЪБЃЌдЫЖЏЭЃжЙЃЌЙ§Еу C зї CHЁЭPQЃЌДЙзуЮЊЕу HЃЌСЌНг BHЃЌдђ BH ГЄЕФзюаЁжЕЮЊ cmЃЈБЃСєзїЭМКлМЃЃЌ жБНгЬюаДНсЙћЃЉЃЎ

ЁОД№АИЁПЃЈ1ЃЉЂйOEЃНOFЃЌжЄУїМћЯъНтЃЛЂкЃНЃЛЃЈ2ЃЉД№АИМћЯъНтЃЛЃЈ3ЃЉ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉЂйЭЈЙ§жЄУїЁїAOEЁеЁїCOFМДПЩХаЖЯOEЃЌOFЕФЪ§СПЙиЯЕЃЛ
ЂкРћгУЦНааЫФБпаЮКЭШЋЕШШ§НЧаЮЕФаджЪЕУЕН![]() ЃЌ
ЃЌ![]() ЃЌШЛКѓРћгУЕШЪНЕФаджЪЧѓНтЃЛ
ЃЌШЛКѓРћгУЕШЪНЕФаджЪЧѓНтЃЛ
ЃЈ2ЃЉжБНгРћгУОиаЮЕФаджЪНсКЯжааФЖдГЦЭМаЮЕФаджЪЕУГіД№АИЃЛ
ЃЈ3ЃЉЩше§ЗНаЮЕФжааФЮЊOЃЌПЩжЄPQОЙ§OЕуЃЎСЌНсOCЃЌШЁOCжаЕуMЃЌСЌНс MHЃЌMBЃЌРћгУе§ЗНаЮЕФаджЪКЭЙДЙЩЖЈРэЧѓГіMBЕФГЄЃЌРћгУжБНЧШ§НЧаЮаББпжаЯпЕШгкаББпвЛАыЧѓГіMHЕФГЄЃЌШЛКѓРћгУСНЕужЎМфЯпЖЮзюЖЬНтОіЮЪЬтМДПЩЃЎ
НтЃКЃЈ1ЃЉЂйЁпЫФБпаЮABCDЪЧЦНааЫФБпаЮЃЌ
ЁрAO=OCЃЌABЁЮCDЃЌ
ЁрЁЯEAO=ЁЯFCOЃЌ
дкЁїEAOКЭЁїFCOжаЃЌ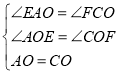
ЁрЁїAOEЁеЁїCOF
ЁрOE=OF
ЙЪД№АИЮЊЃКOE=OFЃЛ
ЂкЁпдк ABCD жаЃЌ![]()
гжгЩЂйПЩжЊЁїAOEЁеЁїCOF
Ёр![]()
Ёр![]()
МДSЫФБпаЮAEFD=SЫФБпаЮCFEB
ЙЪД№АИЮЊЃК=ЃЛ

ЃЈ2ЃЉШчЭМЫљЪОЃК
ЯШевЕНСНИіОиаЮЕФжааФЃЌШЛКѓСЌНгжааФ
жБЯпmМДЮЊЫљЧѓ

ЃЈ3ЃЉЩше§ЗНаЮЕФжааФЮЊOЃЌ
гЩЬтвтПЩжЊPD=BQ
Ёрдке§ЗНаЮABCDжаПЩжЊPQОЙ§OЕуЃЎ
СЌНсOCЃЌШЁOCжаЕуMЃЌСЌНс MHЃЌMBЃЌ
Ёпе§ЗНаЮ ABCD ЕФБпГЄЮЊ 2![]() cm
cm
ЁрCO=BO=![]() ЃЌOM=MC=
ЃЌOM=MC=![]()
Ёр![]()
ЁпCHЁЭPQ
ЁрMH=![]()
BHЁнBM-MH
МДBHЁн![]()
ЁрЕБBЃЌHЃЌMШ§ЕуЙВЯпЪБЃЌBHзюаЁЮЊ![]()
ЙЪД№АИЮЊЃК![]() ЃЎ
ЃЎ



 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌжБЯпABЁЂCDЁЂBCЗжБ№гыЁбOЯрЧагкEЁЂFЁЂGЃЌЧвABЁЮCDЃЌШєOB=6cmЃЌOC=8cmЃЌдђBE+CGЕФГЄЕШгкЃЈ ЃЉ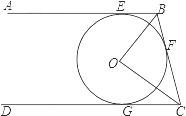
A.13
B.12
C.11
D.10
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкзлКЯЪЕМљПЮЩЯЃЌаЁДЯЫљдкаЁзщвЊВтСПвЛЬѕКгЕФПэЖШЃЌШчЭМЃЌКгАЖEFЁЮMNЃЌаЁДЯдкКгАЖMNЩЯЕуAДІгУВтНЧвЧВтЕУКгЖдАЖаЁЪїCЮЛгкЖЋББЗНЯђЃЌШЛКѓбиКгАЖзпСЫ30УзЃЌЕНДяBДІЃЌВтЕУКгЖдАЖЕчЯпИЫDЮЛгкББЦЋЖЋ30ЁуЗНЯђЃЌДЫЪБЃЌЦфЫћЭЌбЇВтЕУCD=10УзЃЎЧыИљОнетаЉЪ§ОнЧѓГіКгЕФПэЖШЮЊУзЃЎЃЈНсЙћБЃСєИљКХЃЉ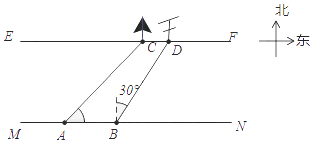
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКдкЦНУцжБНЧзјБъЯЕxOyжаЃЌХзЮяЯпy=ax2+bx+cОЙ§ЕуAЃЈ3ЃЌ0ЃЉЃЌBЃЈ2ЃЌЉ3ЃЉЃЌCЃЈ0ЃЌЉ3ЃЉ
ЃЈ1ЃЉЧѓХзЮяЯпЕФБэДяЪНЃЛ
ЃЈ2ЃЉЩшЕуDЪЧХзЮяЯпЩЯвЛЕуЃЌЧвЕуDЕФКсзјБъЮЊЉ2ЃЌЧѓЁїAODЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЁбOЕФАыОЖЮЊ13ЃЌЯвAB//CDЃЌABЃН24ЃЌCDЃН10ЃЌдђABЁЂCDжЎМфЕФОрРыЮЊЃЈ ЃЉ
A.17
B.7
C.12
D.7Лђ17
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЦНааЫФБпаЮABCDжаЃЌEЃЌFЪЧЖдНЧЯпBDЩЯЕФСНЕуЃЌ ШчЙћЬэМгвЛИіЬѕМўЪЙЁїABEЁеЁїCDFЃЌдђЬэМгЕФЬѕМўВЛФмЪЧЃЈЁЁЁЁЃЉ

A. AE=CF B. BE=FD C. BF=DE D. ЁЯ1=ЁЯ2
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЪЧМИжжУћГЕЕФБъжОЃЌЧыжИГіЃКетМИИіЭМАИжажсЖдГЦЭМаЮгаЃЈ ЃЉ

A.1ИіB.2ИіC.3ИіD.4Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁїABCЕФУцЛ§ЮЊ1ЃЌЗжБ№БЖГЄЃЈбгГЄвЛБЖЃЉABЃЌBCЃЌCAЕУЕНЁїA1B1C1ЃЌдйЗжБ№БЖГЄA1B1ЃЌB1C1ЃЌC1A1ЕУЕНЁїA2B2C2ЃЎЁАДДЫ ЙцТЩЃЌБЖГЄnДЮКѓЕУЕНЕФЁїA2016B2016C2016ЕФУцЛ§ЮЊ__ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌБпГЄЮЊ6ЕФе§СљБпаЮABCDEFЕФЖдГЦжааФгыдЕуOжиКЯЃЌЕуAдкxжсЩЯЃЌЕуBдкЗДБШР§КЏЪ§y=![]() ЮЛгкЕквЛЯѓЯоЕФЭМЯѓЩЯЃЌдђkЕФжЕЮЊЃЈЁЁЁЁЃЉ
ЮЛгкЕквЛЯѓЯоЕФЭМЯѓЩЯЃЌдђkЕФжЕЮЊЃЈЁЁЁЁЃЉ
A.9![]()
B.9![]()
C.3![]()
D.3![]()
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com