
【题目】在综合实践课上,小聪所在小组要测量一条河的宽度,如图,河岸EF∥MN,小聪在河岸MN上点A处用测角仪测得河对岸小树C位于东北方向,然后沿河岸走了30米,到达B处,测得河对岸电线杆D位于北偏东30°方向,此时,其他同学测得CD=10米.请根据这些数据求出河的宽度为米.(结果保留根号)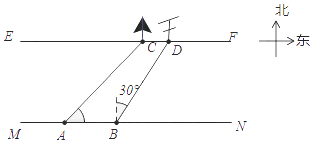
科目:初中数学 来源: 题型:
【题目】已知:A(0,3),B(3,0),C(3,4)三点,点P(x,﹣0.5x),当△ABP的面积等于△ABC的面积时,则P点的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线AB经过点A(6,0)、B(0,6),⊙O的半径为2(O为坐标原点),点P是直线AB上的一动点,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为( )
A.![]()
B.3
C.3 ![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某高楼顶部有一信号发射塔,在矩形建筑物ABCD的A、C两点测得该塔顶端F的仰角分别为45°和60°,矩形建筑物宽度AD=20m,高度DC=30m则信号发射塔顶端到地面的高度(即FG的长)为( )
A.(35 ![]() +55)m
+55)m
B.(25 ![]() +45)m
+45)m
C.(25 ![]() +75)m
+75)m
D.(50+20 ![]() )m
)m
查看答案和解析>>
科目:初中数学 来源: 题型:
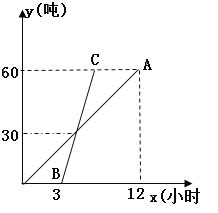
【题目】如图,是甲、乙两种机器人根据电脑程序工作时各自工作量y关于工作时间t的函数图象,线段OA表示甲机器人的工作量y1(吨)关于时间x(时)的函数图象,线段BC表示乙机器人的工作量y2(吨)关于时间a(时)的函数图象,根据图象信息回答下列填空题.
(1) 甲种机器人比乙种机器人早开始工作___ 小时,甲种机器人每小时的工作量是___吨.
(2)直线BC的表达式为 ,当乙种机器人工作5小时后,它完成的工作量是 吨.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△ADE中,AB=AD,AC=AE,∠1=∠2

(1)求证:△ABC≌△ADE;
(2)找出图中与∠1、∠2相等的角(直接写出结论,不需证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载.如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若知道图中阴影部分的面积,则一定能求出( )

A.直角三角形的面积
B.最大正方形的面积
C.较小两个正方形重叠部分的面积
D.最大正方形与直角三角形的面积和
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图 1,在 ABCD 中,AC、BD 交于点 O,过点 O 的直线 l 交 AB 于 E, 交 CD 于 F,①判断 OE 和 OF 的数量关系: ,并证明;
② S四边形AEFD S四边形CFEB (填“>” 或“=” 或“<”).
(2)如图 2 是一块“L”形的材料,请你作一条直线 m,使得直线 m 两边的材料的面积相等(保留作图痕迹,不用证明).
(3)如图 3,正方形 ABCD 的边长为 2![]() cm,动点 P、Q 分别从点 A、C 同时出发,以 相同的速度分别沿 AD、CB 向终点 D、B 移动,当点 P 到达点 D 时,运动停止,过点 C 作 CH⊥PQ,垂足为点 H,连接 BH,则 BH 长的最小值为 cm(保留作图痕迹, 直接填写结果).
cm,动点 P、Q 分别从点 A、C 同时出发,以 相同的速度分别沿 AD、CB 向终点 D、B 移动,当点 P 到达点 D 时,运动停止,过点 C 作 CH⊥PQ,垂足为点 H,连接 BH,则 BH 长的最小值为 cm(保留作图痕迹, 直接填写结果).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点(﹣1,y1),(4,y2)在一次函数y=3x﹣2的图象上,则y1 , y2 , 0的大小关系是( )
A.0<y1<y2
B.y1<0<y2
C.y1<y2<0
D.y2<0<y1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com