
已知:关于x的二次函数 (a>0),点A(n,y1)、B(n+1,y2)、C(n+2,y3)都在这个二次函数的图象上,其中n为正整数.
(a>0),点A(n,y1)、B(n+1,y2)、C(n+2,y3)都在这个二次函数的图象上,其中n为正整数.
(1)y1=y2,请说明a必为奇数;
(2)设a=11,求使y1≤y2≤y3成立的所有n的值;
(3)对于给定的正实数a,是否存在n,使△ABC是以AC为底边的等腰三角形?如果存在,求n的值(用含a的代数式表示);如果不存在,请说明理由.
解:(1)∵点A(n,y1)、B(n+1,y2)都在二次函数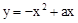 (a>0)的图象上,
(a>0)的图象上,
∴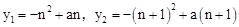 。
。
∵y1=y2,
∴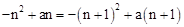 ,整理得:a=2n+1。
,整理得:a=2n+1。
∵n为正整数,∴a必为奇数。
(2)当a=11时,∵y1<y2<y3,
∴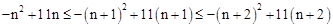 。
。
化简得: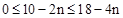 。解得:
。解得: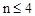 。
。
∵n为正整数,∴n=1、2、3、4。
(3)存在。
假设存在,则AB=AC,
如图所示,过点B作BN⊥x轴于点N,过点A作AD⊥BN于点D,CE⊥BN于点E,
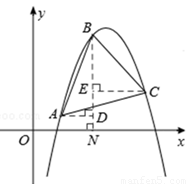
∵xA=n,xB=n+1,xC=n+2,∴AD=CE=1。
在Rt△ABD与Rt△CBE中,AB=BC,AD=CE,
∴Rt△ABD≌Rt△CBE(HL)。
∴∠BAD=∠CBE,即BN为顶角的平分线。
由等腰三角形性质可知,点A、C关于BN对称。
∴BN为抛物线的对称轴,点B为抛物线的顶点,
∴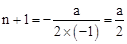 。∴
。∴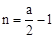 。
。
∴存在n,使△ABC是以AC为底边的等腰三角形,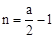 。
。
【解析】(1)将点A和点B的坐标代入二次函数的解析式,利用y1=y2得到用n表示a的式子,即可得到答案;
(2)将a=11代入解析式后,由题意列出不等式组,求得此不等式组的正整数解。
(3)本问为存在型问题,如图所示,可以由三角形全等及等腰三角形的性质,判定点B为抛物线的顶点,点A、C关于对称轴对称,于是得到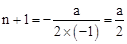 ,从而可以求出
,从而可以求出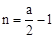 。
。


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
A、a>
| ||||
B、a<0或a>
| ||||
C、a>
| ||||
D、
|
查看答案和解析>>
科目:初中数学 来源: 题型:
 已知关于x的二次函数y=x2+(2k-1)x+k2-1.
已知关于x的二次函数y=x2+(2k-1)x+k2-1.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:北京模拟题 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com