已知:关于x的方程mx2-3(m-1)x+2m-3=0.
(1)求证:m取任何实数量,方程总有实数根;
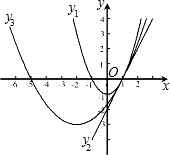
(2)若二次函数y1=mx2-3(m-1)x+2m-3的图象关于y轴对称;
①求二次函数y1的解析式;
②已知一次函数y2=2x-2,证明:在实数范围内,对于x的同一个值,这两个函数所对应的函数值y1≥y2均成立;
(3)在(2)条件下,若二次函数y3=ax2+bx+c的图象经过点(-5,0),且在实数范围内,对于x的同一个值,这三个函数所对应的函数值y1≥y3≥y2均成立,求二次函数y3=ax2+bx+c的解析式.
分析:(1)首先此题的方程并没有明确是一次方程还是二次方程,所以要分类讨论:
①m=0,此时方程为一元一次方程,经计算可知一定有实数根;
②m≠0,此时方程为一元二次方程,可表示出方程的根的判别式,然后结合非负数的性质进行证明.
(2)①由于抛物线的图象关于y轴对称,那么抛物线的一次项系数必为0,可据此求出m的值,从而确定函数的解析式;
②此题可用作差法求解,令y1-y2,然后综合运用完全平方式和非负数的性质进行证明.
(3)根据②的结论,易知y1、y2的交点为(1,0),由于y1≥y3≥y2成立,即三个函数都交于(1,0),结合点(-5,0)的坐标,可用a表示出y3的函数解析式;已知y3≥y2,可用作差法求解,令y=y3-y2,可得到y的表达式,由于y3≥y2,所以y≥0,可据此求出a的值,即可得到抛物线的解析式.
解答:解:(1)分两种情况:
当m=0时,原方程可化为3x-3=0,即x=1;
∴m=0时,原方程有实数根;
当m≠0时,原方程为关于x的一元二次方程,
∵△=[-3(m-1)]
2-4m(2m-3)=m
2-6m+9=(m-3)
2≥0,
∴方程有两个实数根;
综上可知:m取任何实数时,方程总有实数根.
(2)①∵关于x的二次函数y
1=mx
2-3(m-1)x+2m-3的图象关于y轴对称;
∴3(m-1)=0,即m=1;
∴抛物线的解析式为:y
1=x
2-1.
②∵y
1-y
2=x
2-1-(2x-2)=(x-1)
2≥0,
∴y
1≥y
2(当且仅当x=1时,等号成立).
(3)由②知,当x=1时,y
1=y
2=0,即y
1、y
2的图象都经过(1,0);
∵对应x的同一个值,y
1≥y
3≥y
2成立,
∴y
3=ax
2+bx+c的图象必经过(1,0),
又∵y
3=ax
2+bx+c经过(-5,0),
∴y
3=a(x-1)(x+5)=ax
2+4ax-5a;
设y=y
3-y
2=ax
2+4ax-5a-(2x-2)=ax
2+(4a-2)x+(2-5a);
对于x的同一个值,这三个函数对应的函数值y
1≥y
3≥y
2成立,
∴y
3-y
2≥0,
∴y=ax
2+(4a-2)x+(2-5a)≥0;
根据y
1、y
2的图象知:a>0,
∴(4a-2)
2-4a(2-5a)≤0,即(3a-1)
2≤0,
而(3a-1)
2≥0,故a=
∴抛物线的解析式为:y=
x
2+
x-
.
点评:此题主要考查了二次函数与一元二次方程的关系、根的判别式、完全平方公式、非负数的性质以及用待定系数法确定函数解析式的方法,难度较大.



