
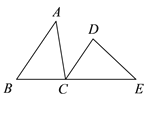
【题目】如图,B、C、E 三点在同一条直线上,AB∥DC,BC=DC,∠ACD=∠E.
求证:(1)∠ACB=∠D;
(2)AB=EC.
科目:初中数学 来源: 题型:
【题目】两条直线都与第三条直线相交,∠1和∠2是内错角,∠3和∠2是邻补角.
(1)根据上述条件,画出符合题意的图形;
(2)若∠1∶∠2∶∠3=1∶2∶3,求∠1,∠2,∠3的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,PB、PC分别是⊙O的切线,切点为B、C,PC、BA的延长线交于点D,DE⊥PO,交PO的延长线于点E. 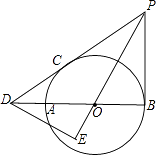
(1)求证:∠DPO=∠EDB;
(2)若PB=3,DB=4,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB,CD被直线EF所截,交点分别为G,H, ∠CHG=∠DHG=![]() ∠AGE.
∠AGE.
(1)CD与EF有怎样的位置关系?请说明理由.
(2)求∠CHG的同位角、内错角、同旁内角的度数.
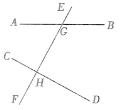
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】体育中考前,抽样调查了九年级学生的“1分钟跳绳”成绩,并绘制成了下面的频数分布直方图(每小组含最小值,不含最大值)和扇形图. 
(1)补全频数分布直方图;
(2)扇形图中m=;
(3)若“1分钟跳绳”成绩大于或等于140次为优秀,则估计全市九年级5900名学生中“1分钟跳绳”成绩为优秀的大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一些半径相同的小圆按如图所示的规律摆放,第1个图形有4个小圆,第2个图形有8个小圆,第3个图形有14个小圆,…,依次规律,第6个图形的小圆个数是( )

A. 56 B. 54 C. 44 D. 42
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明做“用频率估计概率”的实验时,根据统计结果,绘制了如图所示的折线统计图,则符合这一结果的实验最有可能的是( ) 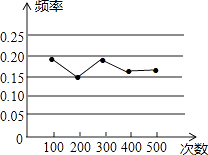
A.同时抛掷两枚硬币,落地后两枚硬币正面都朝上
B.一副去掉大小王的扑克牌,洗匀后,从中任抽一张牌的花色是红桃
C.抛一个质地均匀的正方体骰子,朝上的面点数是3
D.一个不透明的袋子中有4个白球、1个黑球,它们除了颜色外都相同,从中抽到黑球
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对任意一个三位数n,如果n满足各个数位上的数字互不相同,且都不为零,那么称这个数为“相异数”,将一个“相异数”任意两个数位上的数字对调后可以得到三个不同的新三位数,把这三个新三位数的和与111的商记为F(n).例如n=123,对调百位与十位上的数字得到213,对调百位与个位上的数字得到321,对调十位与个位上的数字得到132,这三个新三位数的和为213+321+132=666,666÷111=6,所以F(123)=6.
(1)计算:F(243),F(617);
(2)若s,t都是“相异数”,其中s=100x+32,t=150+y(1≤x≤9,1≤y≤9,x,y都是正整数),规定:k= ![]() ,当F(s)+F(t)=18时,求k的最大值.
,当F(s)+F(t)=18时,求k的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com