
【题目】如图,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() 和
和![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点.
点.
(1)求此抛物线的解析式;
(2)设![]() 是线段
是线段![]() 上的动点,作
上的动点,作![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,当
,当![]() 的面积是
的面积是![]() 面积的2倍时,求
面积的2倍时,求![]() 点的坐标;
点的坐标;
(3)若![]() 为抛物线上
为抛物线上![]() 、
、![]() 两点间的一个动点,过
两点间的一个动点,过![]() 作
作![]() 轴的平行线,交
轴的平行线,交![]() 于
于![]() ,当
,当![]() 点运动到什么位置时,线段
点运动到什么位置时,线段![]() 的值最大,并求此时
的值最大,并求此时![]() 点的坐标.
点的坐标.

【答案】(1)![]() ;(2)点
;(2)点![]() 的坐标为
的坐标为![]() ;(3)当
;(3)当![]() 点的坐标为
点的坐标为![]() 时,线段
时,线段![]() 取最大值.
取最大值.
【解析】
(1)将A、B的坐标代入抛物线的解析式中,求出系数的值,即可求得抛物线的解析式;
(2)△CEF和△BEF同高,则面积比等于底边比,由此可得出CF=2BF;易证得△BEF∽△BAC,根据相似三角形的性质,即可求得BE、AB的比例关系,由此可求出E点坐标;
(3)PQ的长实际是直线AC与抛物线的函数值的差,可设P点横坐标为a,用a表示出P、Q的纵坐标,然后可得出PQ的长与a的函数关系式,根据所得函数的性质即可求出PQ最大时a的值,也就能求出此时P点的坐标.
解:(1)将点![]() ,
,![]() 坐标代入抛物线解析式得:
坐标代入抛物线解析式得:
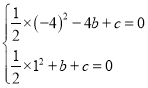 ,
,
解得: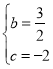 ,
,
![]() 抛物线的解析式为
抛物线的解析式为![]() ;
;
(2)如图,![]() ,
,
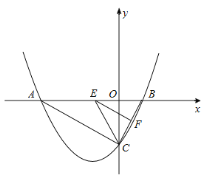
![]() ,则
,则![]() .
.
![]() ,
,
∴![]() ,
,
![]() ,
,
∵![]() 、
、![]() ,
,
则![]() ,
,
∴![]() .
.
![]() 点
点![]() 的横坐标为
的横坐标为![]() ,
,
![]() 点
点![]() 的坐标为
的坐标为![]() ;
;
(3)∵抛物线的解析式为![]() ,
,
当x=0时,y=2,则![]() ,
,
设直线AC的解析式为:![]() ,分别代入
,分别代入![]() 、
、![]() 得:
得:
![]() ,解得:
,解得: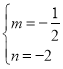 ,
,
∴直线![]() 的解析式为
的解析式为![]() .
.
设![]() 点的坐标为
点的坐标为![]() ,
,
![]() 点是过点
点是过点![]() 作
作![]() 轴的平行线与直线
轴的平行线与直线![]() 的交点,则
的交点,则![]() 点的坐标为
点的坐标为![]() .则有:
.则有:
![]()
![]() ,
,
即当![]() 时,线段
时,线段![]() 取最大值,
取最大值,
此时![]() 点的坐标为
点的坐标为![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,比例规是一种画图工具,它由长度相等的两脚AC和BD交叉构成,利用它可以把线段按一定的比例伸长或缩短.如果把比例规的两脚合上,使螺丝钉固定在刻度3的地方(即同时使OA=3OC,OB=3OD),然后张开两脚,使A,B两个尖端分别在线段a的两个端点上,当CD=1.8cm时,则AB的长为( ) 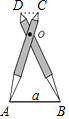
A.7.2 cm
B.5.4 cm
C.3.6 cm
D.0.6 cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着人们生活水平的不断提高,人们对生活饮用水质量要求也越来越高,更多的居民选择购买家用净水器.一商家抓住商机,从生产厂家购进了![]() ,
,![]() 两种型号家用净水器.已知购进2台
两种型号家用净水器.已知购进2台![]() 型号家用净水器比1台
型号家用净水器比1台![]() 型号家用净水器多用200元;购进3台
型号家用净水器多用200元;购进3台![]() 型号净水器和2台
型号净水器和2台![]() 型号家用净水器共用6600元
型号家用净水器共用6600元
(1)求![]() ,
,![]() 两种型号家用净水器每台进价各为多少元?
两种型号家用净水器每台进价各为多少元?
(2)该商家用不超过26400元共购进![]() ,
,![]() 两种型号家用净水器20台,再将购进的两种型号家用净水器分别加价
两种型号家用净水器20台,再将购进的两种型号家用净水器分别加价![]() 后出售,若两种型号家用净水器全部售出后毛利润不低于12000元,求商家购进
后出售,若两种型号家用净水器全部售出后毛利润不低于12000元,求商家购进![]() ,
,![]() 两种型号家用净水器各多少台?(注:毛利润
两种型号家用净水器各多少台?(注:毛利润![]() 售价
售价![]() 进价)
进价)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线1上有A,B两点,AB=12cm,点O是线段AB上的一点,OA=2OB.
(1)OA=______cm,OB=______cm;
(2)若点C是线段AB上一点(点C不与点AB重合),且满足AC=CO+CB,求CO的长;
(3)若动点P,Q分别从A,B同时出发,向右运动,点P的速度为2cm/s,点Q的速度为1cm/s.设运动时间为t(s),当点P与点Q重合时,P,Q两点停止运动.求当t为何值时,2OP-OQ=4(cm);
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明做“用频率估计概率”的试验时,根据统计结果,绘制了如图所示的折线统计图,则符合这一结果的试验最有可能的是( )

A. 任意买一张电影票,座位号是2的倍数的概率
B. 一副去掉大小王的扑克牌,洗匀后,从中任抽一张牌的花色是红桃
C. 抛一个质地均匀的正方体骰子,落下后朝上的面点数是3
D. 一个不透明的袋子中有4个白球、1个黑球,它们除了颜色外都相同,从中抽到黑球
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面一段文字:
问题:0.![]() 能用分数表示吗?
能用分数表示吗?
探求:步骤①设x=0.![]() ,
,
步骤②10x=10×0.![]() ,
,
步骤③10x=8.![]() ,
,
步骤④10x=8+0.![]() ,
,
步骤⑤10x=8+x,
步骤⑥9x=8,
步骤⑦x=![]() .
.
根据你对这段文字的理解,回答下列问题:
(1)步骤①到步骤②的依据是______;
(2)仿照上述探求过程,请你尝试把0.![]() 表示成分数的形式.
表示成分数的形式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC和△DEF,点E在BC边上,点A在DE边上,边EF和边AC相交于点G.如果AE=EC,∠AEG=∠B,那么添加下列一个条件后,仍无法判定△DEF与△ABC一定相似的是( ) 
A.![]() =
= ![]()
B.![]() =
= ![]()
C.![]() =
= ![]()
D.![]() =
= ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在平面直角坐标系中,A(a,0),C(b,2),且满足(a+2)2+![]() =0,过C作CB⊥x轴于B.
=0,过C作CB⊥x轴于B.

(1)求三角形ABC的面积;
(2)如图②,若过B作BD∥AC交y轴于D,且AE,DE分别平分∠CAB,∠ODB,求∠AED的度数;
(3)在y轴上是否存在点P,使得三角形ACP和三角形ABC的面积相等?若存在,求出P点的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com