
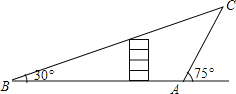
【题目】.如图,小明在大楼的东侧A处发现正前方仰角为75°的方向上有一热气球在C处,此时,小亮在大楼的西侧B处也测得气球在其正前方仰角为30°的位置上,已知AB的距离为60米,试求此时小明、小亮两人与气球的距离AC和BC.(结果保留根号)
科目:初中数学 来源: 题型:
【题目】已知矩形ABCD中,![]() ,
,![]() ,现有两只蚂蚁P和Q同时分别从A、B出发,沿
,现有两只蚂蚁P和Q同时分别从A、B出发,沿![]() 方向前进,蚂蚁P每秒走1cm,蚂蚁Q每秒走2cm.问:
方向前进,蚂蚁P每秒走1cm,蚂蚁Q每秒走2cm.问:
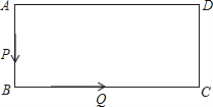

(1)蚂蚁出发后△PBQ第一次是等腰三角形需要爬行几秒?
(2)P、Q两只蚂蚁最快爬行几秒后,直线PQ与边AB平行?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着地铁和共享单车的发展,“地铁+单车”已成为很多市民出行的选择.李华从文化宫站出发,先乘坐地铁,准备在离家较近的A,B,C,D,E中的某一站出地铁,再骑共享单车回家.设他出地铁的站点与文化宫距离为x(单位:千米),乘坐地铁的时间y1(单位:分钟)是关于x的一次函数,其关系如下表:
地铁站 | A | B | C | D | E |
x(千米) | 8 | 9 | 10 | 11.5 | 13 |
y1(分钟) | 18 | 20 | 22 | 25 | 28 |
(1)求y1关于x的函数表达式;
(2)李华骑单车的时间y2(单位:分钟)也受x的影响,其关系可以用y2=![]() x2-11x+78来描述,请问:李华应选择在哪一站出地铁,才能使他从文化宫回到家所需的时间最短?并求出最短时间.
x2-11x+78来描述,请问:李华应选择在哪一站出地铁,才能使他从文化宫回到家所需的时间最短?并求出最短时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,已知点
,已知点![]() 为抛物线第一象限上一动点,连接
为抛物线第一象限上一动点,连接![]() 、
、![]() 、
、![]() .
.
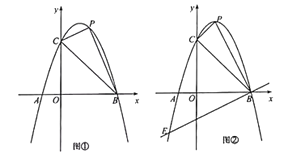
(1)求抛物线的解析式,并直接写出抛物线的顶点坐标;
(2)当![]() 的面积最大时,求出点
的面积最大时,求出点![]() 的坐标;
的坐标;
(3)如图②,当点![]() 与抛物线顶点重合时,过点
与抛物线顶点重合时,过点![]() 的直线
的直线![]() 与抛物线交于点
与抛物线交于点![]() ,在直线
,在直线![]() 上方的抛物线上是否存在一点
上方的抛物线上是否存在一点![]() ,使得
,使得![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD的两条边AB=1,AD=![]() ,以B为旋转中心,将对角线BD顺时针旋转60°得到线段BE,再以C为圆心将线段CD顺时针旋转90°得到线段CF,连接EF,则图中阴影部分面积为_____.
,以B为旋转中心,将对角线BD顺时针旋转60°得到线段BE,再以C为圆心将线段CD顺时针旋转90°得到线段CF,连接EF,则图中阴影部分面积为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, 抛物线![]() 与
与![]() 轴交于点A(-1,0),顶点坐标(1,n)与
轴交于点A(-1,0),顶点坐标(1,n)与![]() 轴的交点在(0,2),(0,3)之间(包 含端点),则下列结论:①
轴的交点在(0,2),(0,3)之间(包 含端点),则下列结论:①![]() ;②
;②![]() ;③对于任意实数m,
;③对于任意实数m,![]() 总成立;④关于
总成立;④关于![]() 的方程
的方程![]() 有两个不相等的实数根.其中结论正确的个数为
有两个不相等的实数根.其中结论正确的个数为![]()
![]()

A. 1 个 B. 2 个 C. 3 个 D. 4 个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接与⊙O,AB是直径,⊙O的切线PC交BA的延长线于点P,OF∥BC交AC于AC点E,交PC于点F,连接AF.
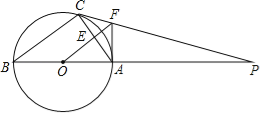
(1)判断AF与⊙O的位置关系并说明理由;
(2)若⊙O的半径为4,AF=3,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一般捕鱼船在A处发出求救信号,位于A处正西方向的B处有一艘救援艇决定前去数援,但两船之间有大片暗礁,无法直线到达.救援艇决定马上调整方向,先向北偏东![]() 方以每小时30海里的速度航行,同时捕鱼船向正北低速航行.30分钟后,捕鱼船到达距离A处
方以每小时30海里的速度航行,同时捕鱼船向正北低速航行.30分钟后,捕鱼船到达距离A处![]() 海里的D处,此时救援艇在C处测得D处在南偏东
海里的D处,此时救援艇在C处测得D处在南偏东![]() 的方向上.
的方向上.
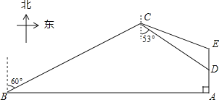
![]() 求C、D两点的距离;
求C、D两点的距离;
![]() 捕鱼船继续低速向北航行,救援艇决定再次调整航向,沿CE方向前去救援,并且捕鱼船和救援艇同达时到E处,若两船航速不变,求
捕鱼船继续低速向北航行,救援艇决定再次调整航向,沿CE方向前去救援,并且捕鱼船和救援艇同达时到E处,若两船航速不变,求![]() 的正弦值.
的正弦值.![]() 参考数据:
参考数据:![]() ,
,![]() ,
,![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com